题目内容
8．
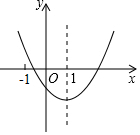如图是二次函数y=ax2+bx+c的图象，其对称轴为直线x=1，则下列结论错误的是（ ）| A． | a＞0 | |
| B． | 2a+b=0 | |
| C． | a-b+c＜0 | |
| D． | 若（$\frac{1}{2}$，y1），（3，y2）是抛物线上两点，则y1＜y2 |
分析 根据抛物线的开口方向、对称轴、二次函数的性质进行判断即可．
解答 解：∵抛物线开口向上，
∴a＞0，A正确，不合题意；
∵对称轴为直线x=1，
∴-$\frac{b}{2a}$=1，即2a+b=0，B正确，不合题意；
当x=-1时，y＞0，
则a-b+c＞0，C错误，符合题意；
当x=$\frac{1}{2}$时，y1＜0，y2＞0，
∴y1＜y2，D正确，不合题意，
故选：C．
点评 本题考查的是二次函数图象与系数的关系，掌握二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定是解题的关键．
练习册系列答案
相关题目
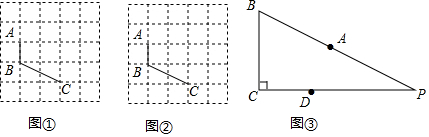
16．
由4个正方体搭成的几何体按如图放置，若要求画出它的三视图，则在所画的俯视图中正方形共有（ ）
由4个正方体搭成的几何体按如图放置，若要求画出它的三视图，则在所画的俯视图中正方形共有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
3．一个不透明的布袋里装有6个黑球和3个白球，它们除颜色外其余都相同，从中任意摸出一个球，是白球的概率为（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
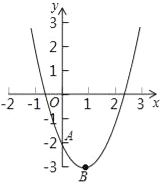已知抛物线y=a（x-1）2-3（a≠0）的图象与y轴交于点A（0，-2），顶点为B．
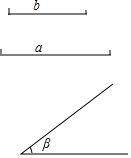画△ABC，使其两边为已知线段a、b，夹角为β．（要求：用尺规作图，写出己知，求作；保留作图痕迹；不在已知的线、角上作图；不写作法）．