题目内容
20.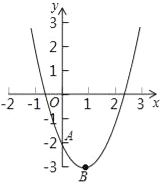 已知抛物线y=a(x-1)2-3(a≠0)的图象与y轴交于点A(0,-2),顶点为B.
已知抛物线y=a(x-1)2-3(a≠0)的图象与y轴交于点A(0,-2),顶点为B.(1)试确定a的值,并写出B点的坐标;
(2)若一次函数的图象经过A、B两点,试写出一次函数的解析式;
(3)试在x轴上求一点P,使得△PAB的周长取最小值.
分析 (1)将点A的坐标代入抛物线的解析式即可求出a的值,根据抛物线的解析式即可求出点B的坐标.
(2)设直线AB的解析式为y=kx+b,然后将点A与B的坐标代入即可求出k与b的值.
(3)由于AB的长度是可求出的,所以△PAB的周长取最小值时,只需要PA+PB最小即可.
解答 解:(1)将A(0,-2)代入y=a(x-1)2-3,
∴-2=a-3
∴a=1
∴抛物线的解析式为:y=(x-1)2-3
∴顶点B(1,-3)
(2)设直线AB的解析式为:y=kx+b,
将点A(0,-2)和B(1,-3)代入y=kx+b,
∴$\left\{\begin{array}{l}{-2=b}\\{-3=k+b}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-1}\\{b=-2}\end{array}\right.$
∴直线AB的解析式为:y=-x-2
(3)设点A关于x轴对称的点为C,
∴C(0,2)
设直线CB的解析式为:y=mx+n,
直线CB与x轴点P,此时△PAB的周长取最小值,
把C(0,2)和B(1,-3)代入y=mx+n,
∴$\left\{\begin{array}{l}{2=n}\\{-3=m+n}\end{array}\right.$
解得:$\left\{\begin{array}{l}{m=-5}\\{n=2}\end{array}\right.$
∴直线CB的解析式为:y=-5x+2
令y=0代入y=-5x+2,
∴x=$\frac{2}{5}$
∴点P的坐标为($\frac{2}{5}$,0)
点评 本题考查一次函数的综合问题,解题的关键是利用待定系数法求出解析式,本题属于中等题型.

练习册系列答案
相关题目
8.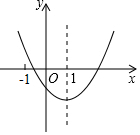 如图是二次函数y=ax2+bx+c的图象,其对称轴为直线x=1,则下列结论错误的是( )
如图是二次函数y=ax2+bx+c的图象,其对称轴为直线x=1,则下列结论错误的是( )
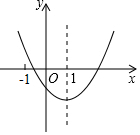 如图是二次函数y=ax2+bx+c的图象,其对称轴为直线x=1,则下列结论错误的是( )
如图是二次函数y=ax2+bx+c的图象,其对称轴为直线x=1,则下列结论错误的是( )| A. | a>0 | |
| B. | 2a+b=0 | |
| C. | a-b+c<0 | |
| D. | 若($\frac{1}{2}$,y1),(3,y2)是抛物线上两点,则y1<y2 |

 小明一家人春节期间参与了“支付宝集五福”活动,小明和姐姐都缺一个“敬业福”,恰巧爸爸有一个可以送给其中一个,两个人各设计了一个游戏,获胜者得到“敬业福”,请用适当的方法说明这两个游戏对小明和姐姐是否公平.
小明一家人春节期间参与了“支付宝集五福”活动,小明和姐姐都缺一个“敬业福”,恰巧爸爸有一个可以送给其中一个,两个人各设计了一个游戏,获胜者得到“敬业福”,请用适当的方法说明这两个游戏对小明和姐姐是否公平.