题目内容
11.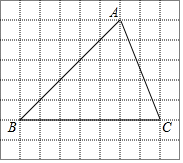 在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )
在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 作AD⊥BC,可得AD=BD=5,利用勾股定理求得AB,再由余弦函数的定义求解可得.
解答 解:如图,作AD⊥BC于点D,
则AD=5,BD=5,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$,
∴cos∠B=$\frac{BD}{AB}$=$\frac{5}{5\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
故选:B.
点评 本题主要考查余弦函数的定义和勾股定理,构建直角三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.若关于x的一元二次方程x2+(k+3)x+2=0的一个根是-1,则另一个根是( )
| A. | 1 | B. | 0 | C. | 2 | D. | -2 |
2.在平面直角坐标系内,把抛物线y=(x-1)2+3向下平移2个单位,那么所得抛物线的解析式是( )
| A. | y=(x-3)2 | B. | y=(x+1)2 | C. | y=(x-1)2+5 | D. | y=(x-1)2+1 |
19.某校初三参加体育测试,一组10人的引体向上成绩如下表:
这组同学引体向上个数的众数与中位数依次是( )
| 完成引体向上的个数 | 7 | 8 | 9 | 10 |
| 人 数 | 1 | 1 | 3 | 5 |
| A. | 9.5和10 | B. | 9和10 | C. | 10和9.5 | D. | 10和9 |
6.-8的绝对值是( )
| A. | -8 | B. | 8 | C. | -$\frac{1}{8}$ | D. | $\frac{1}{8}$ |
16.用科学记数法表示为2.017×103的数是( )
| A. | 2017 | B. | 201.7 | C. | 0.002017 | D. | 20170 |
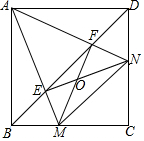 如图,已知正方形ABCD,M,N分别是BC,CD上的点,∠MAN=45°,连接BD分别交AM,AN于E,F,下面结论错误的是⑤.
如图,已知正方形ABCD,M,N分别是BC,CD上的点,∠MAN=45°,连接BD分别交AM,AN于E,F,下面结论错误的是⑤.