题目内容
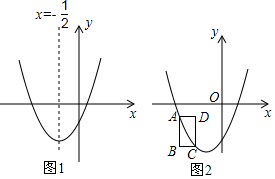
20.已知,直线l:y=kx+b(k≠0)与双曲线y=-$\frac{4}{x}$交于A(x1,y1),B(x2,y2)两点,其中x1≠x2.(1)若k=$\frac{1}{2}$,x1=-4,求直线l的解析式及A、B两点的坐标;
(2)若直线l交x轴于C(x0,0),求证:x1+x2=x0;
(3)若直线a过点D(-2,-2),且与直线y=-$\frac{4}{|x|}$的图象恰好有两个交点,请直接写出直线a的解析式为y=-2.
分析 (1)解方程组得到b=3,太深求得l的解析式为y=$\frac{1}{2}$x+3,根据方程x2+2bx+8=0得x1x2=8,x2=-2,于是得到结论;
(2)根据直线l与x轴交于C(x0,0),当得到x0=-$\frac{b}{k}$,解方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=-\frac{4}{x}}\end{array}\right.$,得到kx2+bx+4=0,于是得到结论;
(3)根据y=-$\frac{4}{|x|}$的图象过点D(-2,-2)根据直线a与函数y=-$\frac{4}{|x|}$的图象恰好有两个交点,于是得到结论.
解答  解:(1)解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x+b}\\{y=-\frac{4}{x}}\end{array}\right.$,
解:(1)解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x+b}\\{y=-\frac{4}{x}}\end{array}\right.$,
∴x2+2bx+8=0,
把x1=-4代入方程得:b=3,
∴l的解析式为y=$\frac{1}{2}$x+3,由
方程x2+2bx+8=0得x1x2=8,x2=-2,
∴A(-4,1),B(-2,2);
(2)直线l:y=kx+b(k≠0)x轴于C(x0,0),
∴x0=-$\frac{b}{k}$,$\left\{\begin{array}{l}{y=kx+b}\\{y=-\frac{4}{x}}\end{array}\right.$,
∴kx2+bx+4=0,x1+x2=-$\frac{b}{k}$,
∴x1+x2=x0;
(3)y=-$\frac{4}{|x|}$的图象为,
∵过点D(-2,-2)的直线a与函数y=-$\frac{4}{|x|}$的图象恰好有两个交点,
如图过直线a的解析式为y=-2,
故答案为:y=-2.
点评 本题考查了反比例函数与一次函数的交点问题,画出图象是解题的关键.

| A. | y=(x-3)2 | B. | y=(x+1)2 | C. | y=(x-1)2+5 | D. | y=(x-1)2+1 |
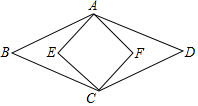 如图,菱形ABCD和正方形AECF,菱形的一个锐角为60度,则菱形ABCD和正方形AECF面积比为( )
如图,菱形ABCD和正方形AECF,菱形的一个锐角为60度,则菱形ABCD和正方形AECF面积比为( )| A. | $\sqrt{3}$:$\sqrt{2}$ | B. | $\sqrt{3}$:1 | C. | 2:1 | D. | 2:$\sqrt{3}$ |
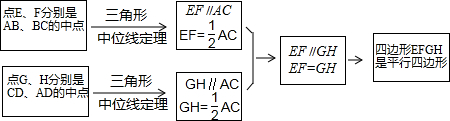
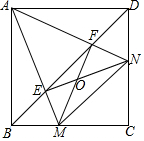 如图,已知正方形ABCD,M,N分别是BC,CD上的点,∠MAN=45°,连接BD分别交AM,AN于E,F,下面结论错误的是⑤.
如图,已知正方形ABCD,M,N分别是BC,CD上的点,∠MAN=45°,连接BD分别交AM,AN于E,F,下面结论错误的是⑤.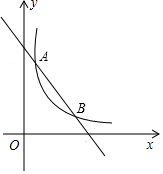 已知直线l:y=-x+5与双曲线y=$\frac{k}{x}$的图象交于A,B两点,且AB=3$\sqrt{2}$.
已知直线l:y=-x+5与双曲线y=$\frac{k}{x}$的图象交于A,B两点,且AB=3$\sqrt{2}$.