题目内容
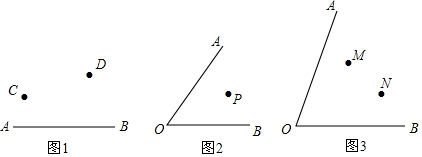
13.如图,直线AB与CD相交于点O,∠AOC=α.(1)如图①,OE平分∠AOD,∠EOF=90°,∠α=30°,求∠BOF的度数;
(2)如图②,∠DOE=$\frac{1}{3}$∠AOD,∠EOF=60°,∠α=30°,求∠BOF的度数;
(3)如图③,∠DOE=$\frac{1}{4}$∠AOD,∠EOF=45°,求$\frac{∠BOF}{∠AOC}$的值.

分析 (1)先根据∠AOC=α=30°,求得∠AOD的度数,再根据OE平分∠AOD,得到∠AOE=$\frac{1}{2}$∠AOD=75°,最后根据∠BOF=180°-∠AOE-∠EOF进行计算即可;
(2)先根据∠AOC=α=30°,求得∠AOD的度数,再根据∠DOE=$\frac{1}{3}$∠AOD,得到∠AOE=$\frac{2}{3}$∠AOD=100°,最后根据∠BOF=180°-∠AOE-∠EOF进行计算即可;
(3)先根据∠AOC=α,求得∠AOD=180°-∠AOC=180°-α,再根据∠DOE=$\frac{1}{4}$∠AOD,得到∠AOE=$\frac{3}{4}$∠AOD=135°-$\frac{3}{4}α$,最后根据∠EOF=45°,求得∠BOF=180°-∠AOE-∠EOF=$\frac{3}{4}$α,进而得到$\frac{∠BOF}{∠AOC}$=$\frac{3}{4}$.
解答  解:(1)如图①,∵∠AOC=α=30°,
解:(1)如图①,∵∠AOC=α=30°,
∴∠AOD=180°-∠AOC=150°,
又∵OE平分∠AOD,
∴∠AOE=$\frac{1}{2}$∠AOD=75°,
又∵∠EOF=90°,
∴∠BOF=180°-∠AOE-∠EOF=180°-75°-90°=15°;
(2)如图②,∵∠AOC=α=30°,
∴∠AOD=180°-∠AOC=150°,
又∵∠DOE=$\frac{1}{3}$∠AOD,
∴∠AOE=$\frac{2}{3}$∠AOD=100°,
又∵∠EOF=60°,
∴∠BOF=180°-∠AOE-∠EOF=180°-100°-60°=20°;
(3)如图③,∵∠AOC=α,
∴∠AOD=180°-∠AOC=180°-α,
又∵∠DOE=$\frac{1}{4}$∠AOD,
∴∠AOE=$\frac{3}{4}$∠AOD=$\frac{3}{4}$(180°-α)=135°-$\frac{3}{4}α$,
又∵∠EOF=45°,
∴∠BOF=180°-∠AOE-∠EOF=180°-(135°-$\frac{3}{4}α$)-45°=$\frac{3}{4}$α,
∴$\frac{∠BOF}{∠AOC}$=$\frac{\frac{3}{4}α}{α}$=$\frac{3}{4}$.
点评 本题主要考查了邻补角的定义以及角平分线的定义的运用,解决问题的关键是根据角的和差关系进行计算.解题时注意:图中两直线相交于点O,则存在多个平角.

 阅读快车系列答案
阅读快车系列答案 如图所示,若△ABE≌△ACF,且AB=5,AE=3,则EC的长为( )
如图所示,若△ABE≌△ACF,且AB=5,AE=3,则EC的长为( )| A. | 2 | B. | 3 | C. | 5 | D. | 2.5 |
 先在给定的数轴上画出下列各数所对应的点:-3,1.5,0,2$\frac{1}{2}$;再将这些数按照从小到大的顺序用“<”号连接起来.
先在给定的数轴上画出下列各数所对应的点:-3,1.5,0,2$\frac{1}{2}$;再将这些数按照从小到大的顺序用“<”号连接起来.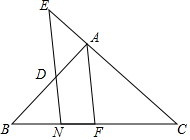 如图,在△ABC中,直线DN平行于中线AF交AB于点D,交AC的延长线于点E,交边BC于点N,求证:$\frac{AD}{AB}$=$\frac{AE}{AC}$.
如图,在△ABC中,直线DN平行于中线AF交AB于点D,交AC的延长线于点E,交边BC于点N,求证:$\frac{AD}{AB}$=$\frac{AE}{AC}$.