题目内容
9.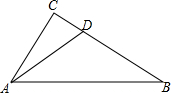 如图,在△ABC中,∠ACB=90°,点D在BC边上,连接AD,若∠CAD=∠B,tan∠DAB=$\frac{3}{4}$,BD=2$\sqrt{5}$,则线段AC的长为$\frac{4}{3}$$\sqrt{5}$.
如图,在△ABC中,∠ACB=90°,点D在BC边上,连接AD,若∠CAD=∠B,tan∠DAB=$\frac{3}{4}$,BD=2$\sqrt{5}$,则线段AC的长为$\frac{4}{3}$$\sqrt{5}$.
分析 过点B作BE⊥AB,交AD的延长线与E,先证明∠CDA=∠CBE,进而可得∠CBE=∠EDB,则根据等角对等边可得DE=BE,然后设BE=3k,AB=4k,则有AE=5k,AD=2k,再证明△CAD∽△CBA,利用相似三角形对应边的比相等的性质求解即可.
解答 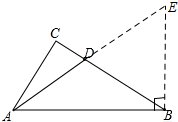 解:过点B作BE⊥AB,交AD的延长线与E,
解:过点B作BE⊥AB,交AD的延长线与E,
∵∠ACB=90°,BE⊥AB,
∴∠CAD+∠CDA=90°,∠ABC+∠CBE=90°,
∵∠CAD=∠ABC,
∴∠CDA=∠CBE,
又∵∠CDA=∠EDB,
∴∠CBE=∠EDB,
∴DE=BE;
∵tan∠DAB=$\frac{3}{4}$,设BE=3k,AB=4k(k≠0),
∴AE=5k,DE=3k,AD=2k,
∵∠C=∠C,∠CAD=∠CBA,
∴△CAD∽△CBA,
∴CA:CB=CD:CA=AD:AB,即CA:(CD+$2\sqrt{5}$)=CD:AC=2k:4k=1:2,
∴AC=2CD,2AC=CD+$2\sqrt{5}$,
解得AC=$\frac{4}{3}\sqrt{5}$,
故答案为:$\frac{4}{3}\sqrt{5}$.
点评 本题考查了相似三角形的判定与性质,勾股定理的应用,解直角三角形等知识,难度适中,正确作出辅助线是解答本题的关键.

练习册系列答案
相关题目
19.将代数式x2+6x-2化成(x+p)2+q的形式为( )
| A. | (x-3)2+11 | B. | (x+3)2-1 | C. | (x+3)2-11 | D. | (x+2)2+4 |
17.下列各等式中正确的是( )
| A. | $\sqrt{4}$=±2 | B. | 2+$\sqrt{3}$=2$\sqrt{3}$ | C. | a2-a-2=(a+1)(a-2) | D. | (am)n=am+n |
4.已知两圆半径分别为1与5,圆心距为4,则这两圆的位置关系是( )
| A. | 内切 | B. | 相交 | C. | 外切 | D. | 外离 |
19.可以用来证明命题“若x2>0.01,则x>0.1”是假命题的反例( )
| A. | 可以是x=-0.2,不可以是 x=0.2 | |
| B. | 可以是x=0.2,不可以是 x=-0.2 | |
| C. | 可以是x=-0.2,也可以是 x=0.2 | |
| D. | 既不可以是x=-0.2,也不可以是 x=0.2 |