题目内容
4．已知两圆半径分别为1与5，圆心距为4，则这两圆的位置关系是（ ）| A． | 内切 | B． | 相交 | C． | 外切 | D． | 外离 |
分析 由两圆的半径分别为1和5，圆心距为4，根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系即可得出两圆位置关系．
解答 解：∵两圆的半径分别为1和5，圆心距为4，
又∵R+r=1+5=6，R-r=5-1=4，圆心距d=R-r=4，
∴两圆的位置关系是内切．
故选：A．
点评 本题主要考查了圆与圆的位置关系．解题的关键是掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
15．下列不等式解法正确的是（ ）
| A． | 如果-$\frac{1}{2}$x＞2，那么x＜-1 | B． | 如果-x＞6，那么x＜6 | ||
| C． | 如果2x＜-2，那么x＞-1 | D． | 如果$-\frac{1}{2}x＜0$，那么x＞0 |
19．
某校为了了解本校七年级学生“双休日”在家的活动情况，对学生进行抽样调查，并将调查结果绘制成如图表：
（1）本次共调查学生50名；
（2）表格中的a=5，这组数据a，26，14，3，2的中位数是5；
（3）在扇形图中，“0～0.5（小时）”对应的扇形的圆心角是36度；
（4）如果该年级有450名学生，那么据此估计大约有126人“双休日”里每日用在上网、看电视的时间为3～4（小时）．
某校为了了解本校七年级学生“双休日”在家的活动情况，对学生进行抽样调查，并将调查结果绘制成如图表：| 每日用在上网、看电视的时间 | 0～0.5（小时） | 1～2（小时） | 3～4（小时） | 5～6（小时） | 7小时以上 |
| 人数 | a | 26 | 14 | 3 | 2 |
（2）表格中的a=5，这组数据a，26，14，3，2的中位数是5；
（3）在扇形图中，“0～0.5（小时）”对应的扇形的圆心角是36度；
（4）如果该年级有450名学生，那么据此估计大约有126人“双休日”里每日用在上网、看电视的时间为3～4（小时）．
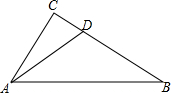如图，在△ABC中，∠ACB=90°，点D在BC边上，连接AD，若∠CAD=∠B，tan∠DAB=$\frac{3}{4}$，BD=2$\sqrt{5}$，则线段AC的长为$\frac{4}{3}$$\sqrt{5}$．
16．（3a+2）（4a2-a-1）的结果中二次项系数是（ ）
| A． | -3 | B． | 8 | C． | 5 | D． | -5 |
14．
甲、乙、丙三人进行飞镖比赛，已知他们每人五次投得的成绩如图，那么三人中成绩最稳定的是（ ）
甲、乙、丙三人进行飞镖比赛，已知他们每人五次投得的成绩如图，那么三人中成绩最稳定的是（ ）| A． | 甲 | B． | 乙 | C． | 丙 | D． | 不确定 |