题目内容
20.计算:(1)$\sqrt{4}-2×{({\frac{1}{2}})^{-1}}+|{-3}|+{(\sqrt{2}-1)^0}$
(2)(2m-1)2+(m-1)(-m-1)
(3)$\frac{x^2}{x-1}-x-1$
(4)$\frac{3-x}{2x-4}÷({x+2-\frac{5}{x-2}})$.
分析 (1)分别根据数的开方法则、0指数幂及负整数指数幂的计算法则、绝对值的性质计算出个各数,再根据实数混合运算的法则进行计算即可;
(2)先去括号,再合并同类项即可;
(3)先通分,再把分子相加减即可;
(4)先算括号里面的,再算除法即可.
解答 解:(1)原式=2-4+3+1
=2;
(2)原式=4m2+1-4m-m2+1
=3m2-4m+2;
(3)原式=$\frac{{x}^{2}}{x-1}$-$\frac{{x}^{2}-1}{x-1}$
=$\frac{1}{x-1}$;
(4)原式=$\frac{3-x}{2(x-2)}$÷$\frac{{x}^{2}-4-5}{x-2}$
=$\frac{3-x}{2(x-2)}$÷$\frac{{x}^{2}-9}{x-2}$
=$\frac{-(x-3)}{2(x-2)}$•$\frac{x-2}{(x+3)(x-3)}$
=-$\frac{1}{2(x+3)}$.
点评 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
15.下列不等式解法正确的是( )
| A. | 如果-$\frac{1}{2}$x>2,那么x<-1 | B. | 如果-x>6,那么x<6 | ||
| C. | 如果2x<-2,那么x>-1 | D. | 如果$-\frac{1}{2}x<0$,那么x>0 |
5.下列各式中,正确的是( )
| A. | $\sqrt{4}=±2$ | B. | $±\sqrt{4}=2$ | C. | $\root{3}{8}=2$ | D. | $\sqrt{{{(-4)}^2}}=-4$ |
10.若一个棱长均为a的三棱柱,它的主视图和俯视图分别是正方形和正三角形,则它的左视图的面积为( )
| A. | $\frac{\sqrt{3}}{2}$a2 | B. | $\frac{\sqrt{3}}{4}$a2 | C. | $\sqrt{3}$a2 | D. | a2 |
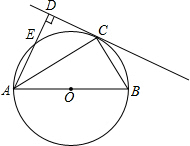 如图,AB为⊙O的直径,过点C作⊙O的切线,AD垂直切线于D,交⊙O于点E.
如图,AB为⊙O的直径,过点C作⊙O的切线,AD垂直切线于D,交⊙O于点E.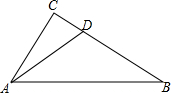 如图,在△ABC中,∠ACB=90°,点D在BC边上,连接AD,若∠CAD=∠B,tan∠DAB=$\frac{3}{4}$,BD=2$\sqrt{5}$,则线段AC的长为$\frac{4}{3}$$\sqrt{5}$.
如图,在△ABC中,∠ACB=90°,点D在BC边上,连接AD,若∠CAD=∠B,tan∠DAB=$\frac{3}{4}$,BD=2$\sqrt{5}$,则线段AC的长为$\frac{4}{3}$$\sqrt{5}$.