题目内容
17. 如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为2$\sqrt{7}$.
如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为2$\sqrt{7}$.
分析 作DF⊥B′E于点F,作B′G⊥AD于点G,首先根据有一个角为60°的等腰三角形是等边三角形判定△BDE是边长为4的等边三角形,从而根据翻折的性质得到△B′DE也是边长为4的等边三角形,从而GD=B′F=2,然后根据勾股定理得到B′G=2$\sqrt{3}$,然后再次利用勾股定理求得答案即可.
解答 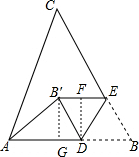 解:如图,作DF⊥B′E于点F,作B′G⊥AD于点G,
解:如图,作DF⊥B′E于点F,作B′G⊥AD于点G,
∵∠B=60°,BE=BD=4,
∴△BDE是边长为4的等边三角形,
∵将△BDE沿DE所在直线折叠得到△B′DE,
∴△B′DE也是边长为4的等边三角形,
∴GD=B′F=2,
∵B′D=4,
∴B′G=$\sqrt{B′{D}^{2}-G{D}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵AB=10,
∴AG=10-6=4,
∴AB′=$\sqrt{A{G}^{2}+B′{G}^{2}}$=$\sqrt{{4}^{2}+(2\sqrt{3})^{2}}$=2$\sqrt{7}$.
故答案为:2$\sqrt{7}$.
点评 本题考查了翻折变换的性质,解题的关键是根据等边三角形的判定定理判定等边三角形,难度不大.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
7.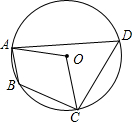 如图,四边形ABCD内接于⊙O,若∠AOC=100°,则∠ABC的大小为( )
如图,四边形ABCD内接于⊙O,若∠AOC=100°,则∠ABC的大小为( )
 如图,四边形ABCD内接于⊙O,若∠AOC=100°,则∠ABC的大小为( )
如图,四边形ABCD内接于⊙O,若∠AOC=100°,则∠ABC的大小为( )| A. | 100° | B. | 50° | C. | 130° | D. | 80° |
12.一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12、10、6、8,则第5组的频率是( )
| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
2.下列几何体中,主视图和俯视图都为矩形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.抛物线y=x2+2x+m-1与x轴有两个不同的交点,则m的取值范围是( )
| A. | m<2 | B. | m>2 | C. | 0<m≤2 | D. | m<-2 |
6.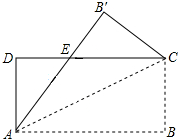 如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
 如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )| A. | ∠DAB′=∠CAB′ | B. | ∠ACD=∠B′CD | C. | AD=AE | D. | AE=CE |
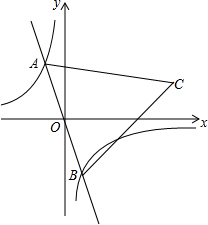 如图,在反比例函数y=-$\frac{2}{x}$的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=$\frac{k}{x}$的图象上运动.若tan∠CAB=2,则k的值为( )
如图,在反比例函数y=-$\frac{2}{x}$的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=$\frac{k}{x}$的图象上运动.若tan∠CAB=2,则k的值为( )