题目内容
6.已知反比例函数$y=\frac{k-1}{x}$图象的两个分支分别位于第一、第三象限.(1)求k的取值范围;
(2)取一个你认为符合条件的K值,写出反比例函数的表达式,并求出当x=-6时反比例函数y的值.
分析 (1)由反比例函数图象过第一、三象限,得到反比例系数k-1大于0,列出关于k的不等式,求出不等式的解集得到k的范围;
(2)根据k的取值范围取k=2,得到y=$\frac{1}{x}$,代入x=-6,求得即可.
解答 解:(1)∵反比例函数图象两支分别位于第一、三象限,
∴k-1>0,
解得:k>1;
(2)∵k>1,
∴取k=2,在反比例函数的表达式为y=$\frac{1}{x}$,
把x=-6代入得,y=$\frac{1}{-6}$=-$\frac{1}{6}$.
点评 此题考查了反比例函数的性质.反比例函数y=$\frac{k}{x}$(k≠0),当k>0时函数图象位于第一、三象限;当k<0时,函数图象位于第二、四象限.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
17. 如图,点E、F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是( )
如图,点E、F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是( )
 如图,点E、F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是( )
如图,点E、F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是( )| A. | AD∥BC | B. | DF∥BE | C. | ∠D=∠B | D. | ∠A=∠C |
1.抛物线y=$\frac{1}{2}$x2的图象向左平移2个单位,在向下平移1个单位,得到的函数表达式为( )
| A. | y=$\frac{1}{2}$x2+2x+1 | B. | y=$\frac{1}{2}$x2+2x-2 | C. | y=$\frac{1}{2}$x2-2x-1 | D. | y=$\frac{1}{2}$x2-2x+1 |
18.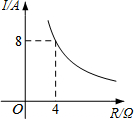 已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,则电流I关于电阻R的函数解析式为( )
已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,则电流I关于电阻R的函数解析式为( )
 已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,则电流I关于电阻R的函数解析式为( )
已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,则电流I关于电阻R的函数解析式为( )| A. | $I=\frac{4}{R}$ | B. | $I=\frac{8}{R}$ | C. | $I=\frac{32}{R}$ | D. | $I=-\frac{32}{R}$ |
15.已知:⊙O是△ABC的外接圆,∠OAB=40°,则∠ACB的大小为( )
| A. | 20° | B. | 50° | C. | 20°或160° | D. | 50°或130° |