题目内容
2.计算:(1)(-2a-2)3b2÷2a-8b-3=$\frac{-4}{{a}^{14}b}$;
(2)(x-1+y-1)-1=$\frac{xy}{x+y}$.
分析 (1)根据积的乘方,可得单项式的除法,根据单项式的除法,可得负整数指数幂,根据负整数指数幂与正整数指数幂互为倒数,可得答案;
(2)根据负整数指数幂与正整数指数幂互为倒数,可得分式,根据分式的性质,可得答案.
解答 解:(1)原式=-8a-6b2÷2a-8b-3=-4a-14b-1=$\frac{-4}{{a}^{14}b}$;
(2)原式=$\frac{1}{{x}^{-1}+{y}^{-1}}$=$\frac{1}{\frac{1}{x}+\frac{1}{y}}$=$\frac{1}{\frac{x+y}{xy}}$=$\frac{xy}{x+y}$,
故答案为:$\frac{-4}{{a}^{14}b}$,$\frac{xy}{x+y}$.
点评 本题考查了负整数指数幂,熟记法则并根据法则计算是解题关键.

练习册系列答案
相关题目
12.若x2+(m-3)x+16是完全平方式,则m的值是( )
| A. | 11 | B. | -5 | C. | ±8 | D. | 11或-5 |
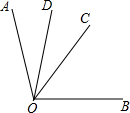 如图,0C是∠A0B的平分线,OD是∠AOC的平分线,且∠BOC+∠COD=75°,求∠BOC和∠COD的度数各是多少度?
如图,0C是∠A0B的平分线,OD是∠AOC的平分线,且∠BOC+∠COD=75°,求∠BOC和∠COD的度数各是多少度?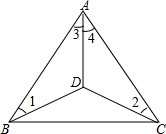 已知,如图△ABC中,BD=DC,∠1=∠2,求证:∠3=∠4.
已知,如图△ABC中,BD=DC,∠1=∠2,求证:∠3=∠4.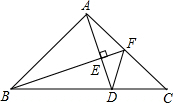 △ABC中,∠BAC=90°,AB=AC,F为AC中点,连接BF作AE⊥BF交BF于E,交BC于D,求证:∠AFB=∠CFD.
△ABC中,∠BAC=90°,AB=AC,F为AC中点,连接BF作AE⊥BF交BF于E,交BC于D,求证:∠AFB=∠CFD.