题目内容
19. 如图,点E是矩形ABCD内任一点,若AB=3,BC=4.则图中阴影部分的面积为6.
如图,点E是矩形ABCD内任一点,若AB=3,BC=4.则图中阴影部分的面积为6.
分析 根据三角形面积公式可知,图中阴影部分面积等于矩形面积的一半;即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴AD=BC=4,
设两个阴影部分三角形的底为AD,BC,高分别为h1,h2,则h1+h2=AB,
∴S△EAB+S△ECD=$\frac{1}{2}$AD•h1+$\frac{1}{2}$BC•h2=$\frac{1}{2}$AD(h1+h2)=$\frac{1}{2}$AD•AB=$\frac{1}{2}$矩形ABCD的面积=$\frac{1}{2}$×3×4=6;
故答案为:6.
点评 本题考查了矩形的性质、三角形面积的计算;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
9.由线段a,b,c组成的三角形是直角三角形的是( )
| A. | a=1,b=1,c=2 | B. | a=$\sqrt{3}$,b=1,c=1 | C. | a=4,b=5,c=6 | D. | a=1,b=2,c=$\sqrt{3}$ |
7.方程2x=0的解是( )
| A. | x=-2 | B. | x=0 | C. | $x=-\frac{1}{2}$ | D. | $x=\frac{1}{2}$ |
4.下面的图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.已知关于x的一元二次方程ax2+bx+c=0(a≠0),则下列判断中不正确的是( )
| A. | 若方程有一根为1,则a+b+c=0 | B. | 若a、c异号,则方程必有解 | ||
| C. | 若b=0,则方程两根互为相反数 | D. | 若c=0,则方程有一根为0 |
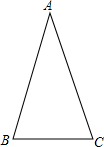 已知,如图,△ABC中,AB=AC,∠A=36°,你能否剪两刀将△ABC分成三个等腰三角形,请将剪痕画在三角形中(至少画出两种剪法,并在图上标出各个角的度数).
已知,如图,△ABC中,AB=AC,∠A=36°,你能否剪两刀将△ABC分成三个等腰三角形,请将剪痕画在三角形中(至少画出两种剪法,并在图上标出各个角的度数).