题目内容
10.已知直线l1、l2、l3互相平行,直线l1与l2的距离是4cm,直线l2与l3的距离是6cm,那么直线l1与l3的距离是10cm或2cm.分析 根据题意,分两种情况:(1)当直线l1与l3在直线l2的同一方向时;(2)当直线l1与l3在直线l2的不同方向时;然后根据直线l1与l2的距离是4cm,直线l2与l3的距离是6cm,求出直线l1与l3的距离是多少即可.
解答 解:(1)当直线l1与l3在直线l2的同一方向时,
l1与l3的距离是:6-4=2(cm).
(2)当直线l1与l3在直线l2的不同方向时,
l1与l3的距离是:6+4=2(cm).
综上,可得直线l1与l3的距离是10cm或2cm.
故答案为:10cm或2cm.
点评 此题主要考查了平行线之间的距离的求法,考查了分类讨论思想的应用,要熟练掌握,解答此题的关键是要明确:从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.在实数$-\frac{2}{3}$,$\sqrt{7}$,0,-$\frac{π}{3}$中,最小的实数是( )
| A. | -$\frac{2}{3}$ | B. | $\sqrt{7}$ | C. | 0 | D. | -$\frac{π}{3}$ |
5.一组样本数据:101,98,102,100,99的方差是( )
| A. | 0 | B. | 1 | C. | 10 | D. | 2 |
15.“创建国家森林城市,打造秀美、和谐祁阳.”某乡镇组织300名干部、群众参加义务植树活动,下表是随机抽出的50名干部、群众义务植树的统计,根据图中的数据回答下列问题:
(1)这50个人平均每人植树4.8棵;
(2)植树棵数的中位数是4.5棵;
(3)植树棵数的众数是4棵;
(4)估计该乡镇本次活动共植树1440棵.
| 植树棵树 | 3 | 4 | 5 | 6 | 8 |
| 人 数 | 10 | 15 | 12 | 7 | 6 |
(2)植树棵数的中位数是4.5棵;
(3)植树棵数的众数是4棵;
(4)估计该乡镇本次活动共植树1440棵.
15.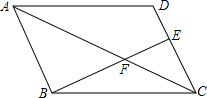 如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( )
如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( )
 如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( )
如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 4:9 |

 如图,点E是矩形ABCD内任一点,若AB=3,BC=4.则图中阴影部分的面积为6.
如图,点E是矩形ABCD内任一点,若AB=3,BC=4.则图中阴影部分的面积为6.