题目内容
11．解不等式组$\left\{\begin{array}{l}\frac{x-1}{2}＜1\\ 3（1-x）≤2x+13\end{array}\right.$，并把它的解集在数轴上表示出来．分析 分别求出不等式组中两不等式的解集，利用不等式组取解集的方法得出原不等式的解集，并将解集表示在数轴上即可．
解答 解：解不等式①得：x＜3
解不等式②得：x≧-2
因此原不等式组的解集为：-2≤x＜3
它的解集在数轴上表示为：
点评 此题考查了一元一次不等式组的解法，不等式组取解集的方法为：“同大取大”；“同小取小”；“大大小小无解”；“大小小大取中间”．
练习册系列答案
相关题目
1．在实数$-\frac{2}{3}$，$\sqrt{7}$，0，-$\frac{π}{3}$中，最小的实数是（ ）
| A． | -$\frac{2}{3}$ | B． | $\sqrt{7}$ | C． | 0 | D． | -$\frac{π}{3}$ |
如图，点E是矩形ABCD内任一点，若AB=3，BC=4．则图中阴影部分的面积为6．
如图，点A在数轴上对应的数为2，若点B也在数轴上，且线段AB的长为4，C为OB的中点，则点C在数轴上对应的数为-1或3．
15．
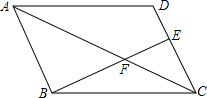如图，在平行四边形ABCD中，点E在CD上，若DE：CE=1：2，则△CEF与△ABF的周长比为（ ）
如图，在平行四边形ABCD中，点E在CD上，若DE：CE=1：2，则△CEF与△ABF的周长比为（ ）| A． | 1：2 | B． | 1：3 | C． | 2：3 | D． | 4：9 |