题目内容
如图,平行四边形ABCD中,AC=AB,延长AC到点P,使CP=AC,BD交AC于E.
(1)求证:BP=2BE;
(2)求证:∠DEC=∠PBA.

(1)求证:BP=2BE;
(2)求证:∠DEC=∠PBA.
考点:平行四边形的性质,全等三角形的判定与性质
专题:证明题
分析:(1)由平行四边形ABCD中,AC=AB,CP=AC,易证得△BCD≌△BCP(SAS),然后由全等三角形的对应边相等,证得BP=BD=2BE;
(2)由全等三角形的对应角相等,可得∠P=∠BDC,继而证得∠P=∠ABD,则可证得结论.
(2)由全等三角形的对应角相等,可得∠P=∠BDC,继而证得∠P=∠ABD,则可证得结论.
解答:证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ACD=∠BAC,
∵AC=AB,CP=AC,
∴CP=CD,∠ACB=∠ABC,
∵∠BCD=∠ACB+∠ACD,∠BCP=∠ABC+∠BAC,
∴∠BCD=∠BCP,
在△BCD和△BCP中,
,
∴△BCD≌△BCP(SAS),
∴BP=BD=2BE;
(2)∵△BCD≌△BCP,
∴∠P=∠BDC,
∵AB∥CD,
∴∠BDC=∠ABD,
∴∠P=∠ABD,
∴∠DEC=∠P+∠EBP=∠ABD+∠EBP=∠PBA.
∴AB=CD,AB∥CD,
∴∠ACD=∠BAC,
∵AC=AB,CP=AC,
∴CP=CD,∠ACB=∠ABC,
∵∠BCD=∠ACB+∠ACD,∠BCP=∠ABC+∠BAC,
∴∠BCD=∠BCP,
在△BCD和△BCP中,
|
∴△BCD≌△BCP(SAS),
∴BP=BD=2BE;
(2)∵△BCD≌△BCP,
∴∠P=∠BDC,
∵AB∥CD,
∴∠BDC=∠ABD,
∴∠P=∠ABD,
∴∠DEC=∠P+∠EBP=∠ABD+∠EBP=∠PBA.
点评:此题考查了平行四边形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
若n边形的内角和比外角和大180°,则n的值为( )
| A、5 | B、6 | C、7 | D、8 |
已知点A(-2,5),点B与点A关于原点O对称,则点B的坐标是( )
| A、(-2,5) |
| B、(-2,-5) |
| C、(2,5) |
| D、(2,-5) |
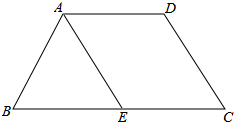 如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠AEB=60°,AB=AD=2cm,则梯形ABCD的周长为( )
如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠AEB=60°,AB=AD=2cm,则梯形ABCD的周长为( )| A、12cm | B、10cm |
| C、8cm | D、6cm |
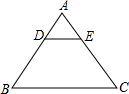 如图,△ABC是等腰三角形,顶点为A、D、E分别在腰AB、AC上,连接DE,若△ADE是等腰三角形,且顶点为A,则下列结论中错误的是( )
如图,△ABC是等腰三角形,顶点为A、D、E分别在腰AB、AC上,连接DE,若△ADE是等腰三角形,且顶点为A,则下列结论中错误的是( )| A、AD=AE |
| B、BD=CE |
| C、DE∥BC |
| D、△ADE≌△ABC |
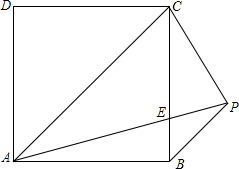 如图,四边形ABCD为正方形,AP=AC,BP∥AC,AP交BC于E,求证:CE=CP.
如图,四边形ABCD为正方形,AP=AC,BP∥AC,AP交BC于E,求证:CE=CP. 如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=
如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=