题目内容
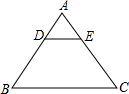 如图,△ABC是等腰三角形,顶点为A、D、E分别在腰AB、AC上,连接DE,若△ADE是等腰三角形,且顶点为A,则下列结论中错误的是( )
如图,△ABC是等腰三角形,顶点为A、D、E分别在腰AB、AC上,连接DE,若△ADE是等腰三角形,且顶点为A,则下列结论中错误的是( )| A、AD=AE |
| B、BD=CE |
| C、DE∥BC |
| D、△ADE≌△ABC |
考点:等腰三角形的性质,平行线的判定,全等三角形的判定
专题:
分析:由△ADE是等腰三角形,且顶点为A,可得AD=AE,判断A正确;由△ABC是等腰三角形,顶点为A,可得AB=AC,又AD=AE,两式相减即可判断B正确;根据等腰三角形的性质及三角形内角和定理,可得∠ADE=∠B,那么DE∥BC,即可判断C正确;由△ADE与△ABC虽然形状相同,但是大小不等可知D错误.
解答:解:A、∵△ADE是等腰三角形,且顶点为A,∴AD=AE,故选项A正确;
B、∵△ABC是等腰三角形,顶点为A,∴AB=AC,又AD=AE,∴BD=CE,故选项B正确;
C、∵AD=AE,AB=AC,∴∠ADE=∠AED,∠B=∠C,又∠A+∠ADE+∠AED=∠A+∠B+∠C,∴∠ADE=∠B,∴DE∥BC,故选项C正确;
D、∵△ADE与△ABC虽然形状相同,但是大小不等,∴△ADE与△ABC不全等,故选项D错误.
故选D.
B、∵△ABC是等腰三角形,顶点为A,∴AB=AC,又AD=AE,∴BD=CE,故选项B正确;
C、∵AD=AE,AB=AC,∴∠ADE=∠AED,∠B=∠C,又∠A+∠ADE+∠AED=∠A+∠B+∠C,∴∠ADE=∠B,∴DE∥BC,故选项C正确;
D、∵△ADE与△ABC虽然形状相同,但是大小不等,∴△ADE与△ABC不全等,故选项D错误.
故选D.
点评:本题考查了等腰三角形的性质,平行线的判定,三角形内角和定理,全等三角形的判定,熟记定理与性质是解题的关键.

练习册系列答案
相关题目
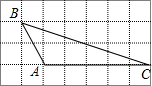 如图,在4×7的正方形网格中,有一个格点三角形ABC,那么∠ABC的正弦值是( )
如图,在4×7的正方形网格中,有一个格点三角形ABC,那么∠ABC的正弦值是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
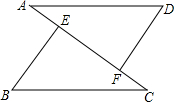 如图,AD∥BC,AD=CB,要使△ADF≌△CBE,需要添加的下列选项中的一个条件是( )
如图,AD∥BC,AD=CB,要使△ADF≌△CBE,需要添加的下列选项中的一个条件是( )| A、AE=CF |
| B、DF=BE |
| C、∠A=∠C |
| D、AE=EF |

 如图,AD平分∠EAC.
如图,AD平分∠EAC.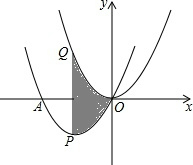 如图,将抛物线y=
如图,将抛物线y=