题目内容
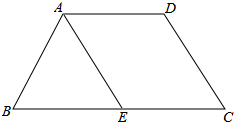如图，等腰梯形ABCD中，AD∥BC，AE∥DC，∠AEB=60°，AB=AD=2cm，则梯形ABCD的周长为（ ）| A、12cm | B、10cm |
| C、8cm | D、6cm |
考点：等腰梯形的性质
专题：
分析：利用等腰梯形的性质以及等边三角形的判定与性质得出AB=BE=EC=AD=CD=2cm，即可得出答案．
解答：解：∵AD∥BC，AE∥DC，
∴四边形AECD是平行四边形，
∴AE=DC，
∵AB=DC，
∴AB=AE，
∵∠AEB=60°，
∴△ABE是等边三角形，
∴AB=BE=AE=2cm，
∵AB=AD=2cm，
∴AB=BE=EC=AD=CD=2cm，
∴梯形ABCD的周长为：10cm．
故选：B．
∴四边形AECD是平行四边形，
∴AE=DC，
∵AB=DC，
∴AB=AE，
∵∠AEB=60°，
∴△ABE是等边三角形，
∴AB=BE=AE=2cm，
∵AB=AD=2cm，
∴AB=BE=EC=AD=CD=2cm，
∴梯形ABCD的周长为：10cm．
故选：B．
点评：此题主要考查了等腰梯形的性质以及等边三角形的判定与性质，得出△ABE是等边三角形是解题关键．
练习册系列答案
相关题目
如图，已知AO⊥OC，OB⊥OD，∠AOB=142°，求∠COD的度数．
如图，是一副普通扑克牌中的13张黑桃牌，将它们洗匀后正面向下放在桌子上，从中任意抽取一张，则抽出的牌点小于6的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图，已知BC是⊙O的直径，过点B的弦BD平行于半径OA，若∠B的度数是50°，则∠C的度数是（ ）| A、50° | B、40° |
| C、30° | D、25° |
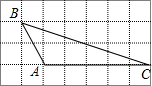如图，在4×7的正方形网格中，有一个格点三角形ABC，那么∠ABC的正弦值是（ ）A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
