Question

10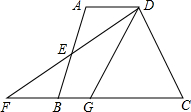．如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点G在边BC上，且∠GDF=∠ADF．
（1）求证：△ADE≌△BFE；
（2）连接EG，判断EG与DF的位置关系并说明理由．
（3）求证：AD+BG=DG．

Answer 1

分析 （1）根据AAS或ASA证明三角形全等；
（2）如图2，EG⊥DF，先证明△DGF是等腰三角形，再根据等腰三角形三线合一的性质得出结论；
（3）由（1）中的全等得对应边AD=BF，再由FG=DG得出结论．

解答 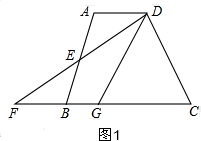解：（1）如图1，∵E是AB的中点，
∴AE=BE，
∵AD∥BC，
∴∠A=∠ABF，∠ADE=∠F，
∴△ADE≌△BFE；
（2）如图2，EG⊥DF，理由是：
∵∠ADF=∠F，∠ADF=∠GDF，
∴∠F=∠GDF，
∴DG=FG，
由（1）得：△ADE≌△BFE，
∴DE=EF，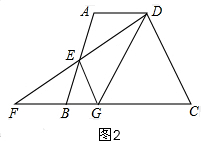
∴EG⊥FD；
（3）如图2，由（1）得：△ADE≌△BFE，
∴AD=BF，
∵FG=BF+BG，
∴FG=AD+BG，
∵FG=DG，
∴AD+BG=DG．

点评 本题考查了全等三角形和等腰三角形的性质和判定，难度不大，熟练掌握全等三角形的判定方法：SSS、SAS、AAS、ASA，明确两直线的位置关系有：①平行，②垂直，本题根据等腰三角形三线合一的性质证明两直线垂直，这在几何证明中经常运用，要熟练掌握．