题目内容
1. 如图,在△ABC中.∠B=60°,⊙0是△ABC的外接圆.过点A的直线交CO的延长线于点P,CP交⊙O于点D,且满足PA2=PD•PC.
如图,在△ABC中.∠B=60°,⊙0是△ABC的外接圆.过点A的直线交CO的延长线于点P,CP交⊙O于点D,且满足PA2=PD•PC.(1)求证:PA为⊙O的切线;
(2)若AC=3,求PD的长.
分析 (1)连接AO,AD,根据PA2=PD•PC可得出△APD∽△CPA,由相似三角形的性质可得出∠PAD=∠PCA,再由圆周角定理得出∠DAC=90°,利用等量代换即可得出结论;
(2)先由圆周角定理得出∠ADC=60°,再由三角形外角的性质得出∠PAD=30°,故可得出AD=PD.根据锐角三角函数的定义求出AD的长,进而可得出结论.
解答 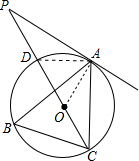 (1)证明:如图,连接AO,AD,
(1)证明:如图,连接AO,AD,
∵PA2=PD•PC,
∴$\frac{PA}{PD}$=$\frac{PC}{PA}$.
∵∠APD=∠CPA,
∴△APD∽△CPA,
∴∠PAD=∠PCA.
∵OD=OA,
∴∠OAD=∠ODA.
∵CD为⊙O的直径,
∴∠DAC=90°,即∠ADC+∠ACD=90°,
∴∠OAD+∠PAD=90°,即∠PAO=90°,
∴PA是⊙O的切线.
(2)解:∵∠B=60°,
∴∠ADC=∠B=60°.
∵∠DAC=90°,
∴∠ACD=30°,即∠PAD=30°,
∴∠P=∠ADC-∠PAD=60°-30°=30°,
∴AD=PD.
在Rt△ADC中,tan∠ADC=$\frac{AC}{AD}$,
∵AC=3,∠ADC=60°,
∴AD=$\frac{AC}{tan∠ADC}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,即PD=$\sqrt{3}$.
点评 本题考查的是相似三角形的判定与性质,根据题意作出辅助线,构造出相似三角形是解答此题的关键.

练习册系列答案
相关题目
6.为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费,超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费,该市某户今年9、10月份的用水量和所交水费如表所示:
设某户每月用水量x(立方米),应交水费y (元).
(1)求a,c的值;
(2)当x≤6,x≥6时,分别写出y与x的函数关系式;
(3)若该户11月份用水量为10立方米,求该户11月份水费是多少元?
设某户每月用水量x(立方米),应交水费y (元).
| 月份 | 用水量(m3) | 收费(元) |
| 9 | 5 | 7.5 |
| 10 | 9 | 27 |
(2)当x≤6,x≥6时,分别写出y与x的函数关系式;
(3)若该户11月份用水量为10立方米,求该户11月份水费是多少元?
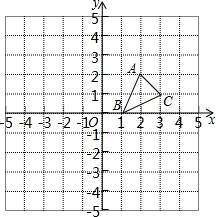 如图,在建立了平面直角坐标系的正方形网格中,A(2,2),B(1,0),C(3,1)
如图,在建立了平面直角坐标系的正方形网格中,A(2,2),B(1,0),C(3,1)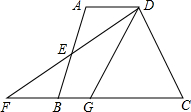 如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.