题目内容
某商店经营T恤衫,已知成批购进的单价是2.5元,在试销中每天的销售量y(件)与销售单价x(元/件)满足下表关系.
(1)试求y与x之间的函数关系;
(2)设商店试售该T恤衫每天获得的毛利额为s,求s与x之间的函数关系;(毛利额=销售总价-成本总价);
(3)当销售单价定为多少时,该商店每天的毛利额最大?此时每天的销售量是多少?
| x(元/件) | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| y(件) | 2000 | 1800 | 1600 | 1400 | 1200 | 1000 | 800 |
(2)设商店试售该T恤衫每天获得的毛利额为s,求s与x之间的函数关系;(毛利额=销售总价-成本总价);
(3)当销售单价定为多少时,该商店每天的毛利额最大?此时每天的销售量是多少?
考点:二次函数的应用
专题:
分析:(1)直接利用待定系数法求出函数解析式即可;
(2)利用毛利额=销售总价-成本总价,得出s与x的函数解析式即可;
(3)直接利用二次函数最值求法得出答案.
(2)利用毛利额=销售总价-成本总价,得出s与x的函数解析式即可;
(3)直接利用二次函数最值求法得出答案.
解答:解:(1)由图表数据可得:每件增加1元,其销量减少200件,
故此函数是一次函数,设解析式为:y=kx+b,
则
,
解得:
.
故y与x之间的函数关系为:y=-200x+3200;
(2)由题意可得:
s=(x-2.5)y
=(x-2.5)(-200x+3200)
=-200x2+3700x-8000;
(3)s=-200x2+3700x-8000=-200(x-
)2+9112.5,
故当销售单价定为
时,该商店每天的毛利额最大,
此时每天的销售量是:y=-200×
+3200=1350(件).
故此函数是一次函数,设解析式为:y=kx+b,
则
|
解得:
|
故y与x之间的函数关系为:y=-200x+3200;
(2)由题意可得:
s=(x-2.5)y
=(x-2.5)(-200x+3200)
=-200x2+3700x-8000;
(3)s=-200x2+3700x-8000=-200(x-
| 37 |
| 4 |
故当销售单价定为
| 37 |
| 4 |
此时每天的销售量是:y=-200×
| 37 |
| 4 |
点评:此题主要考查了二次函数的应用以及二次函数最值求法,根据题意得出函数解析式是解题关键.

练习册系列答案
相关题目
 如图所示,已知∠AOB=∠COD=90°,找出图中其他相等的角及图中互余的角.
如图所示,已知∠AOB=∠COD=90°,找出图中其他相等的角及图中互余的角. 如图,AB为⊙O的直径,DE是⊙O的切线,⊙O过BC上一点D,过D作DE⊥AC于E点,求证:BD=CD.
如图,AB为⊙O的直径,DE是⊙O的切线,⊙O过BC上一点D,过D作DE⊥AC于E点,求证:BD=CD.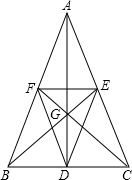 如图,AD、BE、CF是△ABC的中线,G是△ABC的重心.△DEF与△ABC是位似图形吗?并说明理由.
如图,AD、BE、CF是△ABC的中线,G是△ABC的重心.△DEF与△ABC是位似图形吗?并说明理由.