题目内容
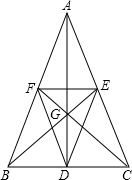 如图,AD、BE、CF是△ABC的中线,G是△ABC的重心.△DEF与△ABC是位似图形吗?并说明理由.
如图,AD、BE、CF是△ABC的中线,G是△ABC的重心.△DEF与△ABC是位似图形吗?并说明理由.考点:位似变换
专题:常规题型
分析:根据三角形中位线性质得EF∥BC,DE∥AB,DF∥AC,EF=
BC,DE=
AB,DF=
AC,则可判断△DEF∽△ABC,加上点G为AD、BE、CF的交点,于是可根据位似图形判断△DEF与△ABC是位似图形.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:△DEF与△ABC是位似图形.理由如下:
∵AD、BE、CF是△ABC的中线,
∴EF、DE、DF为△ABC的中位线,
∴EF∥BC,DE∥AB,DF∥AC,EF=
BC,DE=
AB,DF=
AC,
∴
=
=
,
∴△DEF∽△ABC,
∵点G为AD、BE、CF的交点,
∴△DEF与△ABC是位似图形.
∵AD、BE、CF是△ABC的中线,
∴EF、DE、DF为△ABC的中位线,
∴EF∥BC,DE∥AB,DF∥AC,EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| EF |
| BC |
| DE |
| AB |
| DF |
| AC |
∴△DEF∽△ABC,
∵点G为AD、BE、CF的交点,
∴△DEF与△ABC是位似图形.
点评:本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.注意:两个图形必须是相似形;对应点的连线都经过同一点;对应边平行.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
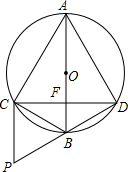 若AC=AD,∠CAD=60°,AB与CD相交于点F,AF=
若AC=AD,∠CAD=60°,AB与CD相交于点F,AF=
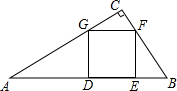 如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上.
如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上. 已知在△ABC中,∠A=90°,AD⊥BC于点D,M为AD中点,BM的延长线交AC于点P,PQ⊥BC于Q.求证:PQ2=PA•PC.
已知在△ABC中,∠A=90°,AD⊥BC于点D,M为AD中点,BM的延长线交AC于点P,PQ⊥BC于Q.求证:PQ2=PA•PC. 如图,已知线段AB=4cm,延长线段AB到C,使BC=2AB.
如图,已知线段AB=4cm,延长线段AB到C,使BC=2AB.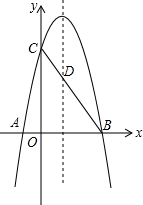 如图,抛物线y=ax2+bx+6与x轴交于A、B两点,与y轴交于点C,已知A(-1,0)、B(3,0).
如图,抛物线y=ax2+bx+6与x轴交于A、B两点,与y轴交于点C,已知A(-1,0)、B(3,0).