题目内容
14.已知整数x满足不等式组$\left\{\begin{array}{l}{2x<3(x-1)}\\{\frac{x-4}{2}<\frac{x-4}{3}+\frac{1}{6}}\end{array}\right.$,则x的算术平方根为2.分析 分别求出各不等式的解集,再求出其公共解集,再公共解集内找出整数x的值,根据算术平方根的定义可得出结论.
解答 解:∵$\left\{\begin{array}{l}2x<3(x-1)①\\ \frac{x-4}{2}<\frac{x-4}{3}+\frac{1}{6}②\end{array}\right.$,由①得,x>3,由②得,x<5,
∴3<x<5.
∵x为整数,
∴x=4,
∴x的算术平方根为:2.
故答案为:2.
点评 本题考查的是一元一次不等式组的整数解,熟知解一元一次不等式的基本步骤是解答此题的关键.

练习册系列答案
相关题目
5.下列各数中,绝对值最大的数是( )
| A. | -3 | B. | -2 | C. | 0 | D. | 2 |
19. 已知二次函数y=x2-5x+6,当自变量x取m时,对应的函数值小于0,当自变量x取m-1、m+1时,对应的函数值为y1、y2,则y1、y2满足( )
已知二次函数y=x2-5x+6,当自变量x取m时,对应的函数值小于0,当自变量x取m-1、m+1时,对应的函数值为y1、y2,则y1、y2满足( )
 已知二次函数y=x2-5x+6,当自变量x取m时,对应的函数值小于0,当自变量x取m-1、m+1时,对应的函数值为y1、y2,则y1、y2满足( )
已知二次函数y=x2-5x+6,当自变量x取m时,对应的函数值小于0,当自变量x取m-1、m+1时,对应的函数值为y1、y2,则y1、y2满足( )| A. | y1>0,y2>0 | B. | y1<0,y2>0 | C. | y1<0,y2<0 | D. | y1>0,y2<0 |
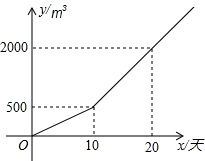 某农户种植一种经济作物,总量用水量y(m3)与种植时间x(天)之间的函数关系如图所示.
某农户种植一种经济作物,总量用水量y(m3)与种植时间x(天)之间的函数关系如图所示. 把一个圆球放置在V形架中,如图是它的平面示意图,CA和CB都是圆O的切线,切点分别是A、B,测得∠ACB=60°,且C点到切点B的距离为6cm,则圆球的半径是2$\sqrt{3}$.
把一个圆球放置在V形架中,如图是它的平面示意图,CA和CB都是圆O的切线,切点分别是A、B,测得∠ACB=60°,且C点到切点B的距离为6cm,则圆球的半径是2$\sqrt{3}$.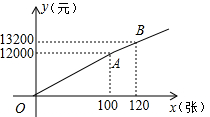 在体育局的策划下,市体育局将组织明星篮球队,为此体育局推出两种购票方案(设购票张数为x,购票总价为y).
在体育局的策划下,市体育局将组织明星篮球队,为此体育局推出两种购票方案(设购票张数为x,购票总价为y).