题目内容
9.计算:(1)$\sqrt{12}-3sin60°+{(π-1)^0}-{2^{-1}}$;
(2)$\frac{x}{x-1}$+$\frac{x^2-6x+9}{3x-x^2}$.
分析 (1)原式第一项化为最简二次根式,第二项利用特殊角的三角函数值计算,第三项利用零指数幂法则计算,最后一项利用负指数幂法则计算即可得到结果;
(2)原式通分并利用同分母分式的加法法则计算即可得到结果,
解答 解:(1)原式=2$\sqrt{3}$-3×$\frac{\sqrt{3}}{2}$+1-$\frac{1}{2}$=$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$;
(2)原式=$\frac{x}{x-1}$-$\frac{(x-3)^{2}}{x(x-3)}$=$\frac{x}{x-1}$-$\frac{x-3}{x}$=$\frac{{x}^{2}-{x}^{2}+4x-3}{x(x-1)}$=$\frac{4x-3}{{x}^{2}-x}$.
点评 此题考查了实数的运算,以及分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
4.虽然近几年无锡市政府加大了太湖水治污力度,但由于大规模、高强度的经济活动和日益增加的污染负荷,使部分太湖水域水质恶化,富营养化不断加剧.为了保护水资源,我市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
| 月用水量(吨) | 单价(元/吨) |
| 不大于10吨部分 | 1.5 |
| 大于10吨不大于m吨部分(20≤m≤50) | 2 |
| 大于m吨部分 | 3 |
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
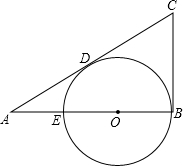 如图,∠B=90°,O是AB上的一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D.若AD=2$\sqrt{3}$,且AB、AE的长是关于x的方程x2-8x+k=0的两个实数根.
如图,∠B=90°,O是AB上的一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D.若AD=2$\sqrt{3}$,且AB、AE的长是关于x的方程x2-8x+k=0的两个实数根. 某校数学兴趣小组要测量天塔CD的高度,如图,他们在点A处测得天塔最高点C的仰角为45°,再往天塔方向前进至点B处测得最高点C的仰角为54°,AB=27m,根据这个兴趣小组测得的数据,计算天塔的高度CD(tan36°≈0.73,结果保留整数).
某校数学兴趣小组要测量天塔CD的高度,如图,他们在点A处测得天塔最高点C的仰角为45°,再往天塔方向前进至点B处测得最高点C的仰角为54°,AB=27m,根据这个兴趣小组测得的数据,计算天塔的高度CD(tan36°≈0.73,结果保留整数).