题目内容
4.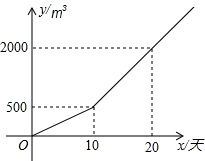 某农户种植一种经济作物,总量用水量y(m3)与种植时间x(天)之间的函数关系如图所示.
某农户种植一种经济作物,总量用水量y(m3)与种植时间x(天)之间的函数关系如图所示.(1)第10天的总用水量为多少?
(2)当x≥10时,求y与x之间的函数关系式.
(3)种植时间为多少天时,总用水量达到6000m3?
分析 (1)由图可知第10天的总用水量为500m3;
(2)设y=kx+b.把已知坐标(10,500),(20,2000)代入解析式即可求解;
(3)若达到6000米3,代入y可得相应的天数.
解答 解:(1)根据图象得出,10天的总用水量为500米3,
(2)当x≥10时,设y=kx+b,
∵函数图象经过点(10,500),(20,2000),
∴$\left\{\begin{array}{l}{10k+b=500}\\{20k+b=2000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=150}\\{b=-1000}\end{array}\right.$,
∴y与x之间的函数关系式为:y=150x-1000;
(3)令y=6000,得150x-1000=6000,
解得:x=$46\frac{2}{3}$.
∴种植时间为46$\frac{2}{3}$天时,总用水量达到6000米3.
点评 此题主要考查了一次函数的应用以及待定系数法求一次函数解析式,正确根据图象得出正确信息是解题关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
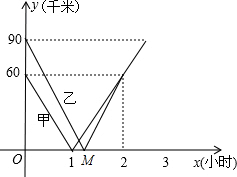 一条笔直的公路上有A、B、C三地,B、C两地相距150千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地,甲、乙两车到A地的距离y1、y2(km)与行驶时间x(h)的关系如图所示,根据图象进行以下探究:
一条笔直的公路上有A、B、C三地,B、C两地相距150千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地,甲、乙两车到A地的距离y1、y2(km)与行驶时间x(h)的关系如图所示,根据图象进行以下探究: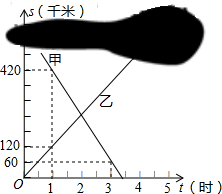 甲、乙两列火车分别从A、B两城同时匀速开出,甲车开往B城,乙车开往A城.由于墨迹覆盖,甲车与乙车据B城的距离s(千米)与时间t(小时)的函数关系部分图象如图所示.
甲、乙两列火车分别从A、B两城同时匀速开出,甲车开往B城,乙车开往A城.由于墨迹覆盖,甲车与乙车据B城的距离s(千米)与时间t(小时)的函数关系部分图象如图所示.