��Ŀ����
8��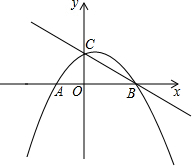 ��ͼ����ƽ��ֱ������ϵ�У�������y=-$\frac{1}{4}{x}^{2}$+$\frac{1}{2}$x+2��x�ύ��A��B���㣬��y�ύ�ڵ�C����P��B������������BA������ÿ��1����λ���ٶ������˶�������P��PQ��x�ᣮֱ��PQ�ֱ���ֱ��BC�������߽��ڵ�Q��K��
��ͼ����ƽ��ֱ������ϵ�У�������y=-$\frac{1}{4}{x}^{2}$+$\frac{1}{2}$x+2��x�ύ��A��B���㣬��y�ύ�ڵ�C����P��B������������BA������ÿ��1����λ���ٶ������˶�������P��PQ��x�ᣮֱ��PQ�ֱ���ֱ��BC�������߽��ڵ�Q��K����1�����߶�KQ�ij���d���P�˶�ʱ��t�ĺ�������ʽ��
��2�����CKQ�����S���ڵ�P�˶�ʱ��t�ĺ�������ʽ��
���� ��1�����ֱ��BC�Ľ���ʽ����������õ�Q��t��-$\frac{1}{2}$t+2����K��t��-$\frac{1}{4}$t2+$\frac{1}{2}t$+2����Ȼ�������������ۼ�����ã�
��2����������õ�C��ֱ��PQ�ľ��룬Ȼ���������������ۼ�����ã�
��� �⣺y=-$\frac{1}{4}{x}^{2}$+$\frac{1}{2}$x+2����x=0ʱ����ã�y=2������OC=2��
��y=0ʱ��0=-$\frac{1}{4}{x}^{2}$+$\frac{1}{2}$x+2����ã�x1=-2��x2=4�����ԣ�OA=2��OB=4��
���ԣ�A��-2��0����B��4��0����C��0��2����
��1����ֱ��BC�Ľ���ʽΪy=kx+b��
����B��C������ã�$\left\{\begin{array}{l}{4k+b=0}\\{b=2}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=-$\frac{1}{2}$x+2��
��PQ��x�ᣬ
�˶�t���Q��t��-$\frac{1}{2}$t+2����K��t��-$\frac{1}{4}$t2+$\frac{1}{2}t$+2����
�൱0��t��4ʱ��d=��-$\frac{1}{4}$t2+$\frac{1}{2}t$+2��-��-$\frac{1}{2}$t+2��=-$\frac{1}{4}$t2+t��
��t��4ʱ��d=��-$\frac{1}{2}$t+2��-��-$\frac{1}{4}$t2+$\frac{1}{2}t$+2��=$\frac{1}{4}$t2-t��
���߶�KQ�ij���d���P�˶�ʱ��t�ĺ�������ʽΪd=$\left\{\begin{array}{l}{-\frac{1}{4}{t}^{2}+t��0��t��4��}\\{{\frac{1}{4}t}^{2}-t��t��4��}\end{array}\right.$��
��2����0��t��4ʱ��C��ֱ��PQ�ľ���Ϊ��4-t����
��S=d��4-t��=��-$\frac{1}{4}$t2+t����4-t��=$\frac{1}{4}$t3-2t2+4t��
��t��4ʱ��C��ֱ��PQ�ľ���Ϊ��t-4����
S=d��t-4��=��-$\frac{1}{4}$t2+t����t-4��=-$\frac{1}{4}$t3+2t2-4t��
�ʡ�CKQ�����S���ڵ�P�˶�ʱ��t�ĺ�������ʽΪS=$\left\{\begin{array}{l}{\frac{1}{4}{t}^{3}-2{t}^{2}+4t��0��t��4��}\\{-\frac{1}{4}{t}^{3}+2{t}^{2}-4t��t��4��}\end{array}\right.$��
���� ���⿼������������x��Ľ��㣬����ϵ������һ�κ����Ľ���ʽ����������˼��������ǽ���Ĺؼ���

 ��У����ϵ�д�
��У����ϵ�д� ��ͼ����ƽ��ֱ������ϵ�У���A��y���ϵ�һ�㣬��B���C��x�����ҹ���ԭ��Գƣ�����A��0��3������B��-4��0����
��ͼ����ƽ��ֱ������ϵ�У���A��y���ϵ�һ�㣬��B���C��x�����ҹ���ԭ��Գƣ�����A��0��3������B��-4��0���� ��ͼ���ڡ�ABC�У�BA=BC����ABC=120�㣬AB�Ĵ�ֱƽ����EF��AB��E����AC��F����֤��AF=$\frac{1}{3}$AC��
��ͼ���ڡ�ABC�У�BA=BC����ABC=120�㣬AB�Ĵ�ֱƽ����EF��AB��E����AC��F����֤��AF=$\frac{1}{3}$AC�� ��ͼ�������������ABC�У�sinB=$\frac{3}{5}$��tanC=3����S��ABC=20����BC�ij���
��ͼ�������������ABC�У�sinB=$\frac{3}{5}$��tanC=3����S��ABC=20����BC�ij���