题目内容
13．一个正多边形的内角和是外角和的2倍，则这个正多边形的每个外角为（ ）| A． | 50° | B． | 60° | C． | 45° | D． | 120° |
分析 先由多边形的内角和和外角和的关系判断出多边形的边数，即可得到结论．
解答 解：设多边形的边数为n．
因为正多边形内角和为（n-2）•180°，正多边形外角和为360°，
根据题意得：（n-2）•180°=360°×2，
解得：n=6．
∴这个正多边形的每个外角=$\frac{360}{6}$=60°，
故选B．
点评 本题考查了正多边形的内角于外角，正六边形的性质；熟练掌握正六边形的性质，求出正多边形的边数是解决问题的关键．
练习册系列答案
相关题目
4．
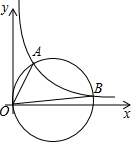如图，点A（1，2）在反比例函数y=$\frac{k}{x}$（x＞0）上，B为反比例函数图象上一点，不与A重合，当以OB为直径的圆经过A点，点B的坐标为（ ）
如图，点A（1，2）在反比例函数y=$\frac{k}{x}$（x＞0）上，B为反比例函数图象上一点，不与A重合，当以OB为直径的圆经过A点，点B的坐标为（ ）| A． | （2，1） | B． | （3，$\frac{2}{3}$） | C． | （4，0.5） | D． | （5，0.4） |
1．
如图所示，直线l1∥l2，三角尺的一个顶点在l2上，若∠1=70°，则∠2=（ ）
如图所示，直线l1∥l2，三角尺的一个顶点在l2上，若∠1=70°，则∠2=（ ）| A． | 70° | B． | 60° | C． | 40° | D． | 30° |
8．
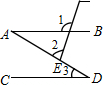如图是婴儿车的平面示意图，其中AB∥CD，∠1=120°，∠2=80°，那么∠3的度数为（ ）
如图是婴儿车的平面示意图，其中AB∥CD，∠1=120°，∠2=80°，那么∠3的度数为（ ）| A． | 40° | B． | 50° | C． | 60° | D． | 70° |
18．一个不透明的口袋中有4个绿球和2个黄球，它们除颜色外其他都完全相同．将球摇匀后，随机摸出一球，吧剩下的球摇匀后，再随机摸出一球，两球都为绿球的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{5}$ | D． | $\frac{2}{5}$ |
5．某市在一次空气污染指数抽查中，收集到10天的数据如下：61，75，70，56，81，91，92，91，75，81．该组数据的中位数是（ ）
| A． | 77.3 | B． | 91 | C． | 81 | D． | 78 |
