题目内容
8．
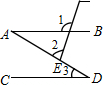如图是婴儿车的平面示意图，其中AB∥CD，∠1=120°，∠2=80°，那么∠3的度数为（ ）| A． | 40° | B． | 50° | C． | 60° | D． | 70° |
分析 根据三角形外角性质求出∠A，根据平行线性质得到∠3=∠A即可．
解答 
解：∵∠1是△AEF的外角，
∴∠A=∠1-∠2=40°，
∵AB∥CD，
∴∠A=∠3=40°，
故选：A．
点评 本题考查了平行线性质和三角形外角性质的应用，关键是求出∠A的度数，根据平行线的性质进行计算．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
18．下列分数中不能化成有限小数的是（ ）
| A． | $\frac{9}{16}$ | B． | $\frac{3}{8}$ | C． | $\frac{5}{18}$ | D． | $\frac{7}{50}$ |
16．若∠A与∠B互为余角，则∠A+∠B=（ ）
| A． | 180° | B． | 120° | C． | 90° | D． | 60° |
3．已知点P（2n-7，4-2n）在第二象限，则n的取值范围是（ ）
| A． | n＜2 | B． | n＞2 | C． | n＜$\frac{7}{2}$ | D． | 2＜n＜$\frac{7}{2}$ |
13．一个正多边形的内角和是外角和的2倍，则这个正多边形的每个外角为（ ）
| A． | 50° | B． | 60° | C． | 45° | D． | 120° |
20．
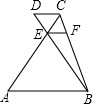如图，AB∥DC，AC与BD 交于点E，EF∥DC交BC于点F，CE=5，CF=4，AE=BC，则$\frac{DC}{AB}$等于（ ）
如图，AB∥DC，AC与BD 交于点E，EF∥DC交BC于点F，CE=5，CF=4，AE=BC，则$\frac{DC}{AB}$等于（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{3}{5}$ |
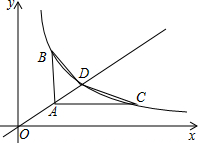直线y=$\frac{2}{3}x$与双曲线y=$\frac{6}{x}$（x＞0）相交于点D．