题目内容
在Rt△ABC中，∠ACB=90°，AB=10cm，AB边上的高为4cm，则Rt△ABC的周长为 cm．
考点：勾股定理
专题：
分析：设AC=b，BC=a，根据勾股定理及三角形的面积公式可列出关于a，b的方程组，求出a+b的值即可．
解答：
解：如图所示，
设AC=b，BC=a，
∵∠ACB=90°，AB=10cm，AB边上的高为4cm，
∴
，解得a+b=6
，
∴Rt△ABC的周长=a+b+10=（6
+10）cm．
故答案为：（6
+10）．
解：如图所示，设AC=b，BC=a，
∵∠ACB=90°，AB=10cm，AB边上的高为4cm，
∴
|
| 5 |
∴Rt△ABC的周长=a+b+10=（6
| 5 |
故答案为：（6
| 5 |
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
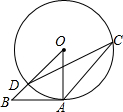如图，AB与圆O相切于点A，且OA=AB，则∠DCA的度数是（ ）| A、45° | B、30° |
| C、60° | D、22.5° |
如图，试探究∠EAB，∠B，∠BCD之间有怎样的关系时，才能使AE∥CD？
将如图所示的点（0，0），（5，4），（3，0），（5，1），（5，-1），（3，0），（4，-2），（0，0），作如下变化：下列命题中，真命题是（ ）
| A、在同一平面内，两条没有交点的射线互相平行 | ||||
| B、三角形的外角大于它的内角 | ||||
C、以
| ||||
D、∠A=
|
若m的倒数是-3，那么m的绝对值是（ ）
| A、3 | ||
B、-
| ||
C、
| ||
| D、-3 |