题目内容
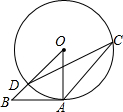如图，AB与圆O相切于点A，且OA=AB，则∠DCA的度数是（ ）| A、45° | B、30° |
| C、60° | D、22.5° |
考点：切线的性质,圆周角定理
专题：
分析：根据切线的性质求得OA⊥AB，进而求得△OAB是等腰直角三角形，得出∠AOD=45°，根据圆周角的性质求得∠DCA的度数．
解答：解：∵AB与圆O相切于点A，
∴OA⊥AB，
∵OA=AB，
∴△OAB是等腰直角三角形，
∴∠AOD=45°，
∴∠ACD=22.5°
故选D．
∴OA⊥AB，
∵OA=AB，
∴△OAB是等腰直角三角形，
∴∠AOD=45°，
∴∠ACD=22.5°
故选D．
点评：本题考查了切线的性质，等腰直角三角形的判定和性质，圆周角定理的应用等，熟练掌握性质定理是解题的关键．
练习册系列答案
怎样学好牛津英语系列答案
导学教程高中新课标系列答案
相关题目
不等式组
的解集为（ ）
|
| A、x＞3 | ||
B、x＞
| ||
| C、x＜3 | ||
D、
|
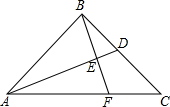如图，在Rt△ABC中，∠ABC=90°，BA=BC，点D为BC边的中点，BE⊥AD于点E，交AC于点F，求
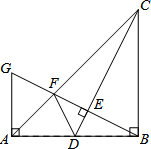如图：在Rt三角形ABC中，∠ABC=90，BA=BC．点D是AB的中点，连接 CD，过点B作BC作垂直CD，分别交CD、CA于点E、F．与过点A且垂直于AB的直线相交于点G，连结DF，给出以下四个结论：（1）
如图，一菱形ABCD的边长为2，且∠ABC=120°，点E是BC的中点，点P为BD上一点，且△PCE的周长最小． 
如图，△ABC中，点D在AB上，点E在AC上，添加一个条件（只写出一种情况），使得△ABC∽△AED并给出你的证明过程．
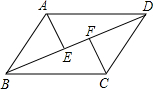如图，已知E、F在BD上，AE⊥BD于E，CF⊥BD于F，AD=BC，BE=DF，请问：△AED与△CFB全等吗？请说说明你的结论．