题目内容
 如图,试探究∠EAB,∠B,∠BCD之间有怎样的关系时,才能使AE∥CD?
如图,试探究∠EAB,∠B,∠BCD之间有怎样的关系时,才能使AE∥CD?考点:平行线的判定
专题:
分析:过B作BF∥AE,先由平行线证出∠A+∠1=180°,再由∠EAB+∠ABC+∠BCD=360°,证出∠2+∠BCD=180°,得出BF∥CD,即可证出AE∥CD.
解答:解:∠EAB+∠ABC+∠BCD=360°时,AE∥CD;
理由如下:过B作BF∥AE,如图所示:
∵BF∥AE,
∴∠A+∠1=180°,
∵∠EAB+∠ABC+∠BCD=360°,
∴∠2+∠BCD=180°,
∴BF∥CD,
∴AE∥CD.
理由如下:过B作BF∥AE,如图所示:

∵BF∥AE,
∴∠A+∠1=180°,
∵∠EAB+∠ABC+∠BCD=360°,
∴∠2+∠BCD=180°,
∴BF∥CD,
∴AE∥CD.
点评:本题考查了平行线的判定与性质的综合运用;培养学生综合运用平行线的性质定理和判定定理解决问题的能力,熟练掌握平行线的判定与性质是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
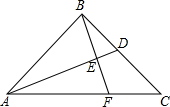 如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D为BC边的中点,BE⊥AD于点E,交AC于点F,求
如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D为BC边的中点,BE⊥AD于点E,交AC于点F,求
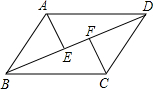 如图,已知E、F在BD上,AE⊥BD于E,CF⊥BD于F,AD=BC,BE=DF,请问:△AED与△CFB全等吗?请说说明你的结论.
如图,已知E、F在BD上,AE⊥BD于E,CF⊥BD于F,AD=BC,BE=DF,请问:△AED与△CFB全等吗?请说说明你的结论. 当∠1,∠2,∠3满足条件
当∠1,∠2,∠3满足条件 如图,在△ABC中,D为BC上一点,BD=CD,AD⊥AC于点A,∠BAD=30°.
如图,在△ABC中,D为BC上一点,BD=CD,AD⊥AC于点A,∠BAD=30°. 如图,在长方体ABCD-A′B′C′D′中,与棱AB平行的有
如图,在长方体ABCD-A′B′C′D′中,与棱AB平行的有 如图,点E是AB,CD外一点,且AB∥CD,∠BED,∠B,∠D又有何关系,并加以说明.
如图,点E是AB,CD外一点,且AB∥CD,∠BED,∠B,∠D又有何关系,并加以说明.