题目内容
在△ABC中,∠A=20°,高BE,CF所在直线交于点O,且O不与B、C重合,则∠BOC= .
考点:三角形内角和定理
专题:分类讨论
分析:本题中因为“高BE、CF所在直线交于点O,且点E、F不与点B、C重合”排除了三角形是直角三角形的可能,所以要分两种情况讨论.
解答: 解:本题要分两种情况讨论如图:
解:本题要分两种情况讨论如图:
①当交点在三角形内部时(如1),在四边形AFOE中,∠AFC=∠AEB=90°,∠A=20°,
根据四边形内角和等于360°得,
∠EOF=180°-∠A=180°-20°=160°.
故∠BOC=160°.
②当交点在三角形外部时(如图2),在△AFC中,∠A=20°,∠AFC=9 0°,
0°,
故∠1=180°-90°-20°=70°,
∵∠1=∠2,
∴在△CEO中,∠2=70°,∠CEO=90°,
∴∠EOF=180°-90°-70°=20°,即∠BOC=20°.
故答案为:160°或20°.
 解:本题要分两种情况讨论如图:
解:本题要分两种情况讨论如图:①当交点在三角形内部时(如1),在四边形AFOE中,∠AFC=∠AEB=90°,∠A=20°,
根据四边形内角和等于360°得,
∠EOF=180°-∠A=180°-20°=160°.
故∠BOC=160°.
②当交点在三角形外部时(如图2),在△AFC中,∠A=20°,∠AFC=9
 0°,
0°,故∠1=180°-90°-20°=70°,
∵∠1=∠2,
∴在△CEO中,∠2=70°,∠CEO=90°,
∴∠EOF=180°-90°-70°=20°,即∠BOC=20°.
故答案为:160°或20°.
点评:本题考查的是三角形内角和定理,在解答此题时要注意进行分类讨论,不要漏解.

练习册系列答案
相关题目
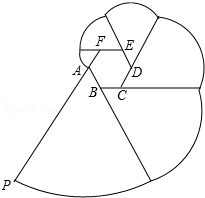 如图,正六边形ABCDEF是边长为2cm的螺母,点P是FA延长线上的点,在A、P之间拉一条长为12cm的无伸缩性细线,一端固定在点A,握住另一端点P拉直细线,把它全部紧紧缠绕在螺母上(缠绕时螺母不动),则点P运动的路径长为
如图,正六边形ABCDEF是边长为2cm的螺母,点P是FA延长线上的点,在A、P之间拉一条长为12cm的无伸缩性细线,一端固定在点A,握住另一端点P拉直细线,把它全部紧紧缠绕在螺母上(缠绕时螺母不动),则点P运动的路径长为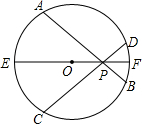 如图,在⊙O中,
如图,在⊙O中,
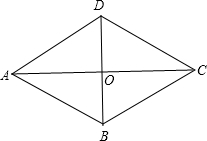 如图,菱形ABCD的周长为2p,对角线AC、BD交于O,AC+BD=q,求菱形ABCD的面积.(提示:利用两数和的平方公式(a+b)2=a2+2ab+b2与勾股定理)
如图,菱形ABCD的周长为2p,对角线AC、BD交于O,AC+BD=q,求菱形ABCD的面积.(提示:利用两数和的平方公式(a+b)2=a2+2ab+b2与勾股定理)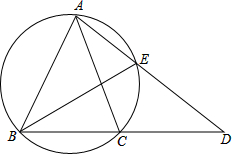 如图,已知E是等腰△ABC外接圆上的点,
如图,已知E是等腰△ABC外接圆上的点, 如图,在平行四边形ABCD中,对角线AC=15cm,BE⊥AC于E,且BE=4cm,若AD=6cm,则AD与BC之间的距离为
如图,在平行四边形ABCD中,对角线AC=15cm,BE⊥AC于E,且BE=4cm,若AD=6cm,则AD与BC之间的距离为