题目内容
16. 已知:如图,在△ABC中,AB=AD=DC,∠BAD=30°;试求∠B和∠C的度数.
已知:如图,在△ABC中,AB=AD=DC,∠BAD=30°;试求∠B和∠C的度数.
分析 由题意,在△ABC中,AB=AD=DC,∠BAD=30°,根据等腰三角形的性质可以求出底角,再根据三角形内角与外角的关系即可求出内角∠C.
解答 解:在△ABC中,AB=AD=DC,
∵AB=AD,在三角形ABD中,
∠B=∠ADB=$\frac{1}{2}$(180°-30°)=75°,
又∵AD=DC,在三角形ADC中,
∴∠C=$\frac{1}{2}$∠ADB=37.5°.
∴∠B=75°,∠C=37.5°.
点评 本题考查等腰三角形的性质及应用等腰三角形两底角相等,还考查了三角形的内角和定理及内角与外角的关系.利用三角形的内角求角的度数是一种常用的方法,要熟练掌握.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
6.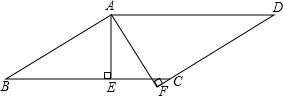 如图,在?ABCD中,AE⊥BC于E,AF⊥DC交DC的延长线于点F,且∠EAF=60°,则∠B等于( )
如图,在?ABCD中,AE⊥BC于E,AF⊥DC交DC的延长线于点F,且∠EAF=60°,则∠B等于( )
 如图,在?ABCD中,AE⊥BC于E,AF⊥DC交DC的延长线于点F,且∠EAF=60°,则∠B等于( )
如图,在?ABCD中,AE⊥BC于E,AF⊥DC交DC的延长线于点F,且∠EAF=60°,则∠B等于( )| A. | 60° | B. | 50° | C. | 70° | D. | 65° |
7.代数式$-\frac{3}{2}x$,$\frac{5}{x-y}$,$-x+\frac{y}{2}$,$\frac{{7{y^2}}}{3x}$,$\frac{2a}{2b}$,$-\frac{9}{7}$中是分式的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.下列运算中,正确的是( )
| A. | a2•a6=a12 | B. | (a3)3=a6 | C. | (-2a)3=6a3 | D. | (a2)3=a6 |
6.下列各式不是多项式x3-x的因式的是( )
| A. | x | B. | 3x-1 | C. | x-1 | D. | x+1 |
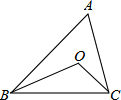 已知:如图:△ABC中,∠B、∠C的角平分线交于点O,若∠A=60°,则∠BOC=120°.
已知:如图:△ABC中,∠B、∠C的角平分线交于点O,若∠A=60°,则∠BOC=120°.



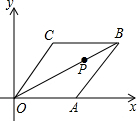 如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4)点P的对角线OB上一个动点,点D的坐标为(0,-2),当DP与AP之和最小时,点P的坐标为($\frac{4}{3}$,$\frac{2}{3}$).
如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4)点P的对角线OB上一个动点,点D的坐标为(0,-2),当DP与AP之和最小时,点P的坐标为($\frac{4}{3}$,$\frac{2}{3}$).