题目内容
19. 如图,在平行四边形ABCD中,以AC为斜边作Rt△ACE,又∠BED=90°.求证:AC=BD.
如图,在平行四边形ABCD中,以AC为斜边作Rt△ACE,又∠BED=90°.求证:AC=BD.
分析 连接EO,首先根据平行四边形的性质可得AO=CO,BO=DO,即O为BD和AC的中点,在Rt△AEC中EO=$\frac{1}{2}$AC,在Rt△EBD中,EO=$\frac{1}{2}$BD,进而得到AC=BD,再根据对角线相等的平行四边形是矩形可证出结论.
解答  证明:连接EO,
证明:连接EO,
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
在Rt△EBD中,
∵O为BD中点,
∴EO=$\frac{1}{2}$BD,
在Rt△AEC中,∵O为AC中点,
∴EO=$\frac{1}{2}$AC,
∴AC=BD.
点评 此题主要考查了平行四边形的性质,直角三角形斜边上的中线,关键是掌握直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
7.代数式$-\frac{3}{2}x$,$\frac{5}{x-y}$,$-x+\frac{y}{2}$,$\frac{{7{y^2}}}{3x}$,$\frac{2a}{2b}$,$-\frac{9}{7}$中是分式的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.下列运算中,正确的是( )
| A. | a2•a6=a12 | B. | (a3)3=a6 | C. | (-2a)3=6a3 | D. | (a2)3=a6 |
 甲骑摩托车从A地去B地,乙开汽车从B地丢A地,同时出发.匀速行驶.各自列达终点后停止.设甲、乙两人间距离为S(单位:千米),甲行驶的时间为t(单位:小时).变量s与t之间的关系如图所示.
甲骑摩托车从A地去B地,乙开汽车从B地丢A地,同时出发.匀速行驶.各自列达终点后停止.设甲、乙两人间距离为S(单位:千米),甲行驶的时间为t(单位:小时).变量s与t之间的关系如图所示.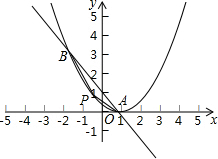 如图,已知抛物线y1=$\frac{1}{3}{x}^{2}$+bx+c和直线y2=kx+h都经过A(1,0),B(-2,3)两点.
如图,已知抛物线y1=$\frac{1}{3}{x}^{2}$+bx+c和直线y2=kx+h都经过A(1,0),B(-2,3)两点.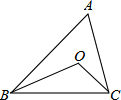 已知:如图:△ABC中,∠B、∠C的角平分线交于点O,若∠A=60°,则∠BOC=120°.
已知:如图:△ABC中,∠B、∠C的角平分线交于点O,若∠A=60°,则∠BOC=120°.