题目内容
7. 如图,一副分别含有30°和45°角的两个直角三角板,拼成如图的图示的图形,则∠BFD的度数是( )
如图,一副分别含有30°和45°角的两个直角三角板,拼成如图的图示的图形,则∠BFD的度数是( )| A. | 15° | B. | 25 | C. | 30° | D. | 10° |
分析 先根据直角三角板的性质得出∠B及∠CDE的度数,再由补角的定义得出∠BDF的度数,根据三角形内角和定理即可得出结论.
解答 解:∵图中是一副直角三角板,
∴∠B=45°,∠CDE=60°,
∴∠BDF=180°-60°=120°,
∴∠BFD=180°-45°-120°=15°.
故选A.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
17.等式(a+1)0=1的条件是( )
| A. | a≠-1 | B. | a≠0 | C. | a≠1 | D. | a=-1 |
18.下面能够成直角三角形三边长的是( )
| A. | 5,6,7 | B. | 5,12,13 | C. | 1,4,9 | D. | 5,11,12 |
15.若关于x的不等式(a+1)x>a+1的解集是x<1,则a的取值范围是( )
| A. | a<-1 | B. | a>-1 | C. | a<1 | D. | a<0 |
2.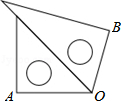 一副三角板如图所示放置,则∠AOB=( )
一副三角板如图所示放置,则∠AOB=( )
 一副三角板如图所示放置,则∠AOB=( )
一副三角板如图所示放置,则∠AOB=( )| A. | 60° | B. | 75° | C. | 105° | D. | 180° |
16.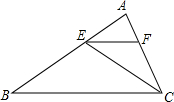 如图,CE是△ABC的角平分线,EF∥BC,交AC于点F.已知∠AFE=64°,则∠FEC的度数为( )
如图,CE是△ABC的角平分线,EF∥BC,交AC于点F.已知∠AFE=64°,则∠FEC的度数为( )
 如图,CE是△ABC的角平分线,EF∥BC,交AC于点F.已知∠AFE=64°,则∠FEC的度数为( )
如图,CE是△ABC的角平分线,EF∥BC,交AC于点F.已知∠AFE=64°,则∠FEC的度数为( )| A. | 64° | B. | 32° | C. | 36° | D. | 26° |
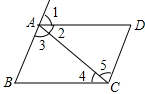 已知,如图,∠1=∠ABC=∠ADC,∠3=∠5,∠2=∠4,∠ABC+∠BCD=180°,将下列推理过程补充完整:
已知,如图,∠1=∠ABC=∠ADC,∠3=∠5,∠2=∠4,∠ABC+∠BCD=180°,将下列推理过程补充完整: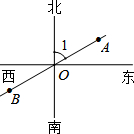 如图,已知A、B、O三点在同一条直线上,∠1=60°,则射线OA是表示北偏东60°方向的一条射线;射线OB是表示南偏西60°方向的一条射线.
如图,已知A、B、O三点在同一条直线上,∠1=60°,则射线OA是表示北偏东60°方向的一条射线;射线OB是表示南偏西60°方向的一条射线.