如图.CE是△ABC的角平分线.EF∥BC.交AC于点F．已知∠AFE=64°.则∠FEC的度数为( )A．64°B．32°C．36°D．26° 题目和参考答案——青夏教育精英家教网—

题目内容

16．

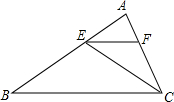如图，CE是△ABC的角平分线，EF∥BC，交AC于点F．已知∠AFE=64°，则∠FEC的度数为（　　）

A．

64°

B．

32°

C．

36°

D．

26°

分析先根据平行线的性质求出∠ACB的度数，再由CE是△ABC的角平分线得出∠ECF的度数，根据三角形外角的性质即可得出结论．

解答解：∵EF∥BC，∠AFE=64°，
∴∠ABC=∠AFE=64°．
∵CE是△ABC的角平分线，
∴∠ECF=$\frac{1}{2}$∠ACB=$\frac{1}{2}$×64°=32°，
∴∠FEC=∠AFE-∠ECF=64°-32°=32°．
故选B．

点评本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．

练习册系列答案

相关题目

a²•a³=a⁶

（a²）²=a⁴

7．

如图，一副分别含有30°和45°角的两个直角三角板，拼成如图的图示的图形，则∠BFD的度数是（　　）

4．若x²+2x的值是8，则4x²-5+8x的值是27．

11．计算：
（1）（-1）¹⁰¹+（π-3）⁰+（$\frac{1}{2}$）^-1-$\sqrt{（1-\sqrt{2}）^{2}}$．
（2）$\frac{3}{{\sqrt{3}}}$-（$\sqrt{3}$）²+${（π+\sqrt{3}）^0}$-$\sqrt{27}$+$|{\sqrt{3}-2}|$．

1．

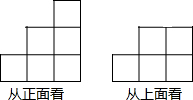由一些大小相同的小正方体组成的简单几何体从正面和上面看到的形状图象如图所示．
（1）请画出这个几何体的一种从左面看到的形状图；
（2）如果设组成这个几何体的小正方体的块数为n，请你写出n的所有可能的值．

8．-2x+y=1，用含x的式子表示y，得y=2x+1．

5．$\frac{{-1+\sqrt{5}}}{2}$的绝对值等于$\frac{-1+\sqrt{5}}{2}$，倒数等于$\frac{\sqrt{5}+1}{2}$．

6．

试题分类