题目内容
16.半径为2的圆内接正三角形,正四边形,正六边形的边心距之比为1:$\sqrt{2}$:$\sqrt{3}$.分析 根据题意可以求得半径为2的圆内接正三角形,正四边形,正六边形的边心距,从而可以求得它们的比值.
解答 解:由题意可得,
正三角形的边心距是:2×sin30°=2×$\frac{1}{2}$=1,
正四边形的边心距是:2×sin45°=2×$\frac{\sqrt{2}}{2}=\sqrt{2}$,
正六边形的边心距是:2×sin60°=2×$\frac{\sqrt{3}}{2}=\sqrt{3}$,
∴半径为2的圆内接正三角形,正四边形,正六边形的边心距之比为:1:$\sqrt{2}$:$\sqrt{3}$,
故答案为:1:$\sqrt{2}$:$\sqrt{3}$.
点评 本题考查正多边形和圆,解答本题的关键是明确题意,求出相应的图形的边心距.

练习册系列答案
相关题目
6.通过调查,一段时间内,C、D两城生产化肥供给A、B两乡,其中A、B两乡需求总量y(吨)与化肥市场价格x(百元/吨)(3≤x≤8),存在下列关系:
C、D两城生产总量Z(吨)与化肥市价x(百元/吨)成正比例函数:Z=100x,已知C城生产总量为240吨,A乡需求量为200吨.如果需求量y与生产量Z相等,此时处于平衡状态.
(1)请通过描点画图,探究y与x之间的函数关系;
(2)某运输公司承担化肥运输任务,已知从C城运往A、B两乡运费分别为20元/t和15元/t;从D城运往A、B两乡费用分别未能25元/t和24元/t,当市场处于平衡状态时,如何调运可使总费用最少?并求出最小费用是多少元?
| x | 4 | 5 | 6 | 7 |
| y | 550 | 500 | 450 | 400 |
(1)请通过描点画图,探究y与x之间的函数关系;
(2)某运输公司承担化肥运输任务,已知从C城运往A、B两乡运费分别为20元/t和15元/t;从D城运往A、B两乡费用分别未能25元/t和24元/t,当市场处于平衡状态时,如何调运可使总费用最少?并求出最小费用是多少元?
11.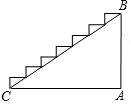 某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
 某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )| A. | 3.5sin29°米 | B. | 3.5cos29°米 | C. | 3.5tan29°米 | D. | $\frac{3.5}{cos29°}$米 |
6.多边形的外角和等于( )
| A. | 180° | B. | 360° | C. | 720° | D. | (n-2)•180° |
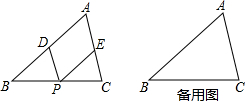 在△ABC中,点P是BC上一动点(与B、C不重合),过点P作PD∥AC交AB于D.作PE∥AB交AC于E,则四边形AEPD是平行四边形.
在△ABC中,点P是BC上一动点(与B、C不重合),过点P作PD∥AC交AB于D.作PE∥AB交AC于E,则四边形AEPD是平行四边形.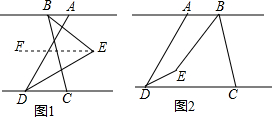

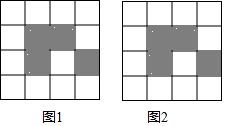 如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.