题目内容
7.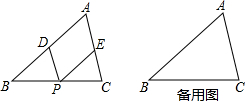 在△ABC中,点P是BC上一动点(与B、C不重合),过点P作PD∥AC交AB于D.作PE∥AB交AC于E,则四边形AEPD是平行四边形.
在△ABC中,点P是BC上一动点(与B、C不重合),过点P作PD∥AC交AB于D.作PE∥AB交AC于E,则四边形AEPD是平行四边形.(1)当P运动到何处时,?AEPD是菱形,说明理由.
(2)根据(1)的研究成果,将一张三角形纸片折叠两次,折出一个菱形的四个顶点,再顺次连结成菱形,在备用图中画出两条折线,并作简要说明.
分析 (1)根据有一组邻边相等的平行四边形是菱形进行判断即可;
(2)先折出角平分线AP,再折出AP的中垂线,即可得到菱形的四个顶点.
解答 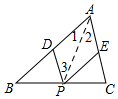 解:(1)当AP平分∠BAC时,即点P在∠BAC的平分线与BC的交点位置时,四边形AEPD为菱形,理由如下:
解:(1)当AP平分∠BAC时,即点P在∠BAC的平分线与BC的交点位置时,四边形AEPD为菱形,理由如下:
当AP平分∠BAC时,∠1=∠2,
∵AC∥DP,
∴∠3=∠2,
∴∠1=∠3,
∴AD=PD,
又∵PD∥AC,PE∥AB,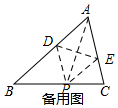
∴四边形ADPE是平行四边形,
∴四边形ADPE是菱形;
(2)如图所示,先把∠BAC对折,折痕AP即为∠BAC的平分线,即AP为第一条折痕;
再则AP的中垂线,使A与P重合,DE为第二条折痕;
连接DP,EP,则四边形ADPE为菱形.
点评 本题主要考查了菱形的判定,利用轴对称进行作图以及平行四边形的判定的综合应用,解题时注意:有一组邻边相等的平行四边形是菱形.

练习册系列答案
相关题目
17.二次函数y=2x2-2x+m(0<m<$\frac{1}{2}$),如果当x=a时,y<0,那么当x=a+1时,函数值y的取值范围为( )
| A. | y<0 | B. | 0<y<m | C. | m<y<m+4 | D. | y>m |
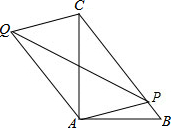 如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,点P为BC上任意一点,连接PA,以PA、PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为$\frac{24}{5}$.
如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,点P为BC上任意一点,连接PA,以PA、PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为$\frac{24}{5}$. 如图,已知BD是△ABC的角平分线,DE∥AB交BC于E,EF∥AC交AB于F.
如图,已知BD是△ABC的角平分线,DE∥AB交BC于E,EF∥AC交AB于F.
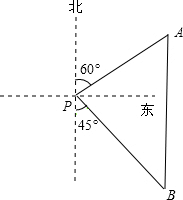 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时,B处与灯塔P的距离约为102n mile.(结果取整数,参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时,B处与灯塔P的距离约为102n mile.(结果取整数,参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)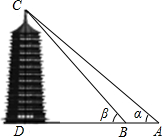 一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为$\frac{tanα•tanβ•s}{tanβ-tanα}$米.
一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为$\frac{tanα•tanβ•s}{tanβ-tanα}$米. 如图,直线a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB:BC=1:2,DE=3,则EF的长为6.
如图,直线a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB:BC=1:2,DE=3,则EF的长为6.