题目内容
15. 已知,如图,△ABC中,AB=AC,AE=CD,BE交AD于点P,∠BAC=∠C=60°,
已知,如图,△ABC中,AB=AC,AE=CD,BE交AD于点P,∠BAC=∠C=60°,(1)求证:∠1=∠2;
(2)求∠BPD的度数.
分析 (1)根据全等三角形的判定与性质,可得答案;
(2)根据三角形外角的性质,可得答案.
解答 (1)证明:在△ABE和△CAD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠ACD=60°}\\{AE=CD}\end{array}\right.$,
∴△ABE≌△CAD (SAS),
∴∠1=∠2;
(2)∵∠BPD是△ABP的外角,
∴∠BPD=∠2+∠BAP.
∵∠1=∠2,
∴∠BPD=∠1+∠BAP=∠BAC=60°,
∠BPD的度数是60°.
点评 本题考查了全等三角形的判定与性质,利用三角形外角的性质得出∠BPD=∠2+∠BAP是解题关键.

练习册系列答案
相关题目
6.按下列图示的程序计算,若开始输入的值为x=2,则最后输出的结果是( )


| A. | 6 | B. | 21 | C. | 156 | D. | 231 |
10.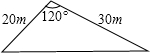 某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
 某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )| A. | $450\sqrt{3}a$元 | B. | $225\sqrt{3}a$元 | C. | $150\sqrt{3}a$元 | D. | $300\sqrt{3}a$ |
5.已知⊙O的半径是10,直线l是⊙O的切线,则圆心O到直线l的距离是( )
| A. | 2.5 | B. | 3 | C. | 5 | D. | 10 |
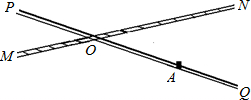 如图,铁路MN和公路PQ在点O处交汇,∠QON=30°,在点A处有一栋居民楼,AO=200m,如果火车行驶时,周围200m以内会受到噪音的影响,那么火车在铁路MN上沿ON方向行驶时,居民楼是否会受到噪音的影响?如果火车行驶的速度为72km/h,居民楼受噪音影响的时间约为多少秒(精确到0.1s)?
如图,铁路MN和公路PQ在点O处交汇,∠QON=30°,在点A处有一栋居民楼,AO=200m,如果火车行驶时,周围200m以内会受到噪音的影响,那么火车在铁路MN上沿ON方向行驶时,居民楼是否会受到噪音的影响?如果火车行驶的速度为72km/h,居民楼受噪音影响的时间约为多少秒(精确到0.1s)?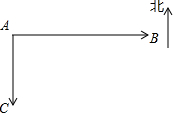 如图,甲船以15千米/小时的速度从港口A向正南方向航行,同时乙船以20千米/小时的速度从港口B向港口A方向航行.已知港口B在港口A的正东方向,且相距80千米.则行驶2小时后两船相距50千米.
如图,甲船以15千米/小时的速度从港口A向正南方向航行,同时乙船以20千米/小时的速度从港口B向港口A方向航行.已知港口B在港口A的正东方向,且相距80千米.则行驶2小时后两船相距50千米.