题目内容
15．如果y=$\sqrt{2x-16}$+$\sqrt{8-x}$+16，那么$\frac{x+y}{\sqrt{2x}}$+$\frac{x-y}{\sqrt{y}}$的值是多少？分析 利用非负数的性质求得x、y的值，然后代入求解即可．
解答 解：∵$\sqrt{2x-16}$≥0，$\sqrt{8-x}$≥0，
∴2x-16=0，8-x=0，
∴x=8，
∴y=0+0+16=16，
∴$\frac{x+y}{\sqrt{2x}}$+$\frac{x-y}{\sqrt{y}}$=$\frac{8+16}{\sqrt{2×8}}$+$\frac{8-16}{\sqrt{16}}$=$\frac{24}{4}$+$\frac{-8}{4}$=6-2=4．
点评 本题考查了二次根式的化简求值的知识，解题的关键是能够利用非负数的性质求得x和y的值，难度不大．
练习册系列答案
相关题目
某校食堂为了给住宿生快速提供早餐，把不同的品种搭配成5种价格不同的套餐出售．小明调查了他所在班50名同学某一天购买早餐的情况（每人购买一份），并绘制了如图的条形统计图，条形框上的百分数是购买该种套餐的人数占全班人数的百分数．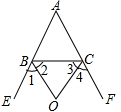
若O是△ABC外一点，OB、OC分别平分△ABC的外角∠CBE、∠BCF，若∠A=n°，画出图形并用n的代数表示∠BOC．