题目内容
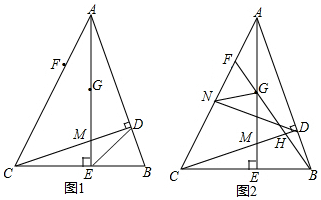
4.问题情境:如图1,边长为16cm正方形ABCD中,E为AB边上一个动点,折叠该正方形,使D点与E点重合,点C落在点F处,折痕分别与AD、BC交于点M、N,EF与BC交于点G,连接DE交MN于点H.自主探究:
如图2,小颖研究了点E是AB中点的情形:
(1)请直接写出线段AM的长度为6cm,△BEG的周长为32cm;
(2)猜想线段MN与DE之间的关系,并证明你的结论.
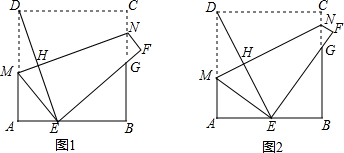
分析 (1)设AM=x,则DM=ME=16-x,在RT△AME中利用勾股定理即可求出AM,利用△AEM∽△BGE得$\frac{AE}{BG}$=$\frac{AM}{BE}$=$\frac{EM}{GE}$求出BG、EG即可求出△EBG的周长.
(2)如图2中,结论MN=DE.理由如下,作NK⊥AD于K,只要证明△ADE≌△KNM即可.
解答 (1)解:如图1中,∵四边形ABCD是正方形,
∴AB=AD=16,∠A=∠B=∠ADC=90°,
∵四边形MNFE是由四边形MNCD翻折得到,
∴DM=ME,∠MDC=∠MEF=90°,设AM=x,则DM=ME=16-x,
∵AE=EB=8,
在RT△AME中,∵ME2=AM2+AE2,
∴(16-x)2=x2+82,
∴x=6,
∴AM=6,ME=10,
∵∠AEM+∠BEG=90°,∠BEG+∠BGE=90°,
∴∠AEM=∠BGE,
∵∠A=∠B,
∴△AEM∽△BGE,
∴$\frac{AE}{BG}$=$\frac{AM}{BE}$=$\frac{EM}{GE}$,
∴$\frac{8}{BG}$=$\frac{6}{8}$=$\frac{10}{EG}$
∴BG=$\frac{32}{3}$,EG=$\frac{40}{3}$,
∴△EBG周长为8+$\frac{32}{3}$+$\frac{40}{3}$=32.
故答案分别为6,32.
(2)如图2中,结论MN=DE.理由如下,
作NK⊥AD于K,
∵∠KDC=∠DCN=∠DKN=90°,
∴四边形CDKN是矩形,
∴CD=KN=AD,
∵∠AED+∠ADE=90°,∠KMN+∠ADE=90°,
∴∠AED=∠KMN,
在△ADE和△KNM中,
$\left\{\begin{array}{l}{∠AED=∠KMN}\\{∠A=∠MKN=90°}\\{AD=KN}\end{array}\right.$,
∴△ADE≌△KNM,
∴DE=MN.
点评 本题考查翻折变换、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识解题的关键是正确寻找全等三角形或相似三角形,利用全等三角形或相似三角形的性质解决问题,属于中考常考题型.

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
| 锻炼情况 | 女生 | 男生 |
| 天天锻炼 | 20 | 27 |
| 不经常锻炼 | 18 | 24 |
| 不锻炼 | 12 | 9 |
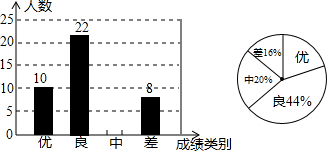
(2)男生中,每种情况的男生各占百分之几?然后根据计算结果绘制男生参加体育锻炼情况的扇形统计图.
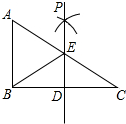 如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于$\frac{1}{2}$BC长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=$\frac{1}{2}$AB中,正确的个数为( )
如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于$\frac{1}{2}$BC长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=$\frac{1}{2}$AB中,正确的个数为( )