题目内容
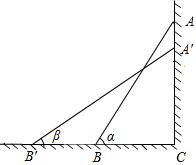 如图,AB是斜靠在墙上的长梯,AB与地面的夹角为α,当梯顶A下滑1m至A′时,梯脚B滑至B′,A′B′与地面的夹角为β,若tanα=
如图,AB是斜靠在墙上的长梯,AB与地面的夹角为α,当梯顶A下滑1m至A′时,梯脚B滑至B′,A′B′与地面的夹角为β,若tanα=| 4 |
| 3 |
| 3 |
| 5 |
考点:解直角三角形的应用
专题:
分析:通过解直角△ABC求得AC的长度;通过解直角△A′B′C求得A′C的长度;然后由AA′=AC-A′C=1来求AB的长度.
解答: 解:依题意知,AB=A′B′.
解:依题意知,AB=A′B′.
∵tanα=
,
∴sinα=
.
在Rt△ABC中,∠ABC=α,则sinα=
.故AC=
AB.
在△ABC中,∠A′B′C=β,则sinβ=
.故A′C=
A′B′=
AB.
依题意得,AA′=AC-A′C=1,即
AB-
AB=1,
解得 AB=5.
答:AB的长度是5m.
 解:依题意知,AB=A′B′.
解:依题意知,AB=A′B′.∵tanα=
| 4 |
| 3 |
∴sinα=
| 4 |
| 5 |
在Rt△ABC中,∠ABC=α,则sinα=
| AC |
| AB |
| 4 |
| 5 |
在△ABC中,∠A′B′C=β,则sinβ=
| A′C |
| A′B′ |
| 3 |
| 5 |
| 3 |
| 5 |
依题意得,AA′=AC-A′C=1,即
| 4 |
| 5 |
| 3 |
| 5 |
解得 AB=5.
答:AB的长度是5m.
点评:本题考查了解直角三角形的应用,此题利用长梯的长度不变进行解答的.

练习册系列答案
相关题目
已知一组数据12,5,9,5,14,下列说法不正确的是( )
| A、中位数是9 | B、众数是5 |
| C、极差是9 | D、平均数是8 |
关于x的方程(a-3)x2+x+2a-1=0是一元二次方程的条件是( )
| A、a≠0 | ||
| B、a≠3 | ||
C、a≠
| ||
| D、a≠-3 |
下列四个函数中,y随x的增大而减小的是( )
| A、y=4x |
| B、y=2x+5 |
| C、y=x-7 |
| D、y=-x+2 |
 如图,在抛物线y=x2上取一点P,在x轴上取一点A,使OP=PA,过点A作x轴的垂线与直线OP交于点Q,当△APQ为正三角形时,试求△APQ的面积.
如图,在抛物线y=x2上取一点P,在x轴上取一点A,使OP=PA,过点A作x轴的垂线与直线OP交于点Q,当△APQ为正三角形时,试求△APQ的面积.