题目内容
4.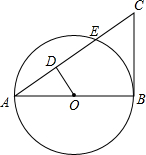 如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点E,D为AC上一点,∠AOD=∠C.
如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点E,D为AC上一点,∠AOD=∠C.(1)求证:OD⊥AC;
(2)若AE=8,AB=10,求OD的长.
分析 (1)根据切线的性质得出∠ABC=90°,进而得出∠A+∠C=90°,再由∠AOD=∠C,可得∠AOD+∠A=90°,即可证明;
(2)由垂径定理可得,D为AE中点,根据已知可利用勾股定理求出.
解答 (1)证明:∵BC是⊙O的切线,AB为⊙O的直径
∴∠ABC=90°,
∴∠A+∠C=90°,
又∵∠AOD=∠C,
∴∠AOD+∠A=90°,
∴∠ADO=90°,
∴OD⊥AC;
(2)解:∵OD⊥AE,O为圆心,
∴D为AE中点,AE=8,
∴AD=$\frac{1}{2}$AE=4,
∵AO=$\frac{1}{2}$AB=5,
∴OD=$\sqrt{{AO}^{2}{-AD}^{2}}$=3.
点评 此题主要考查了圆的切线性质,及解直角三角形的知识和垂径定理的应用等知识,利用OD⊥AE,O为圆心,得出D为AE中点,再利用解直角三角形知识是解决问题的关键.

练习册系列答案
相关题目
9.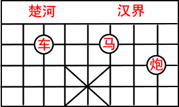 如图,已知棋子“车”的坐为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )
如图,已知棋子“车”的坐为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )
 如图,已知棋子“车”的坐为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )
如图,已知棋子“车”的坐为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )| A. | (2,3) | B. | (3,2) | C. | (-2,-3) | D. | (-3,2) |
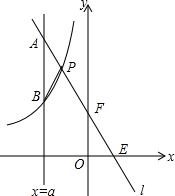 如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{2}{x}$(x<0)交于点P(-1,n),且F是PE的中点.
如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{2}{x}$(x<0)交于点P(-1,n),且F是PE的中点.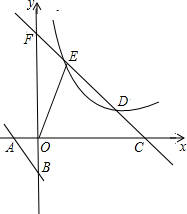 如图,直线l:y=-2x-2与x轴、y轴分别交于A、B两点,向右平移直线l交第一象限内双曲线y=$\frac{k}{x}$于D、E,交x轴正半轴于C,CD交y轴于F点,若CD=AB,S△EOC=12,则k的值为6.
如图,直线l:y=-2x-2与x轴、y轴分别交于A、B两点,向右平移直线l交第一象限内双曲线y=$\frac{k}{x}$于D、E,交x轴正半轴于C,CD交y轴于F点,若CD=AB,S△EOC=12,则k的值为6.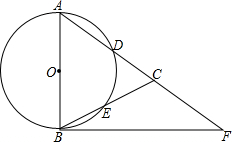 如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且BF是⊙O的切线.
如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且BF是⊙O的切线.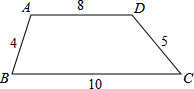 在四边形ABCD中,AD∥BC,AB与CD不平行,根据图中数据,若BA、CD延长后交于点M,则△MBC的周长为55.
在四边形ABCD中,AD∥BC,AB与CD不平行,根据图中数据,若BA、CD延长后交于点M,则△MBC的周长为55. 甲骑车到乙家研讨数学问题,中途因等候红灯停止了一分钟,之后又骑行了1.2千米到达了乙家.若甲骑行的速度始终不变,从出发开始计时,剩余的路程S(单位:千米)与时间t(单位:分钟)的函数关系的图象如图所示,则图中a等于( )
甲骑车到乙家研讨数学问题,中途因等候红灯停止了一分钟,之后又骑行了1.2千米到达了乙家.若甲骑行的速度始终不变,从出发开始计时,剩余的路程S(单位:千米)与时间t(单位:分钟)的函数关系的图象如图所示,则图中a等于( )