题目内容
15.耩(jiǎng)子是一种传统农用播种的工具,大小款式不一,图(1)是改良后有轮子的一种,图(2)是其示意图,现测得AC=40cm,∠C=30°,∠BAC=45°.为了使耩子更牢固,AB处常用粗钢筋制成,则制作此耩子时需要准备多长的粗钢筋?(结果保留根号)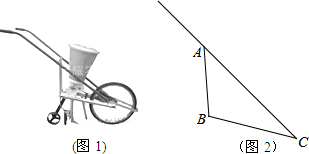
分析 过点B作BD⊥AC于D.设BD=x,在Rt△ABD中和Rt△CBD中,分别求出AB和CD的值,再利用条件AD+CD=AC,即x+$\sqrt{3}$x=40,解方程求出x的值,进而求出AB的值.
解答  解:过点B作BD⊥AC于D.设BD=x,
解:过点B作BD⊥AC于D.设BD=x,
在Rt△ABD中,∠BAC=45°,
∴BD=AD=x,AB=$\sqrt{2}$x,
在Rt△CBD中,∠ACB=30°,
∴CD=$\sqrt{3}$x,
∵AD+CD=AC,
∴x+$\sqrt{3}$x=40,
∴x=20$\sqrt{3}$-20,
∴AB=$\sqrt{2}$x=20$\sqrt{6}$-20$\sqrt{2}$.
答:制作此耩子时需准备(20$\sqrt{6}$-20$\sqrt{2}$)cm的粗钢筋.
点评 本题考查了解直角三角形的应用,解直角三角形的一般过程是:①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.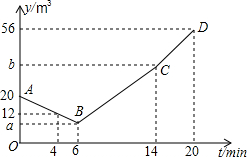 水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.
水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.
(1)每个出水口每分钟出水1m3,表格中a=8;
(2)求进水口每分钟的进水量和b的值;
(3)在整个过程中t为何值时,水池有水16m3
 水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.
水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.(1)每个出水口每分钟出水1m3,表格中a=8;
(2)求进水口每分钟的进水量和b的值;
(3)在整个过程中t为何值时,水池有水16m3
| 时间 | 池中有水(m3) |
| 12:00 | 20 |
| 12:04 | 12 |
| 12:06 | a |
| 12:14 | b |
| 12:20 | 56 |
20.已知关于x的方程kx2+(1-k)x-1=0,下列说法正确的是( )
| A. | 当k≠0时,方程总有两个不相等的实数解 | |
| B. | 当k=-1时,方程有两个相等的实数解 | |
| C. | 当k=1时,方程有一个实数解 | |
| D. | 当k=0时,方程无解 |
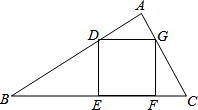 如图,正方形DEFG内接于△ABC,且△ADG、△BDE、△CFG的面积分别为1、3、1,则正方形DEFG的面积是4.
如图,正方形DEFG内接于△ABC,且△ADG、△BDE、△CFG的面积分别为1、3、1,则正方形DEFG的面积是4.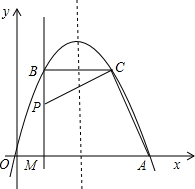 如图,经过原点的抛物线y=-x2+mx(m>2)与x轴的另一交点为A,过点P(1,$\frac{m}{2}$)作直线PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连接CB,CP,CA,要使得CA⊥CP,则m的值为3.
如图,经过原点的抛物线y=-x2+mx(m>2)与x轴的另一交点为A,过点P(1,$\frac{m}{2}$)作直线PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连接CB,CP,CA,要使得CA⊥CP,则m的值为3. 如图,l1∥l2∥l3,AB:BC=2:3,DF=15,求DE、EF的长度.
如图,l1∥l2∥l3,AB:BC=2:3,DF=15,求DE、EF的长度.