题目内容
20．已知关于x的方程kx2+（1-k）x-1=0，下列说法正确的是（ ）| A． | 当k≠0时，方程总有两个不相等的实数解 | |
| B． | 当k=-1时，方程有两个相等的实数解 | |
| C． | 当k=1时，方程有一个实数解 | |
| D． | 当k=0时，方程无解 |
分析 利用k的值，分别代入求出方程的根的情况即可．
解答 解：关于x的方程kx2+（1-k）x-1=0，
A、取k=-1，则-x2+2x-1=0，则-（x-1）2=0，此时方程有两个相等的实数解，故此选项错误；
B、当k=-1时，-x2+2x-1=0，则-（x-1）2=0，此时方程有两个相等的实数解，故此选项正确；
C、当k=1时，x2-1=0方程有两个实数解，故此选项错误；
D、当k=0时，x-1=0，则x=1，故此选项错误；
故选：B．
点评 本题考查了根的判别式与一元一次方程的解，代入k的值判断方程根的情况是解题的关键．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
如图，二次函数y=-$\frac{\sqrt{3}}{3}{x}^{2}-\frac{2}{3}\sqrt{3}x+\sqrt{3}$的图象交x轴于A，B两点，交y轴于点C，顶点为D．
12．在四张完全相同的卡片上分别印有等边三角形、平行四边形、等腰梯形、圆的图案，现将印有图案的一面朝下，混合后从中随机抽取一张，则抽到的卡片上印有的图案是轴对称图形的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{4}$ |
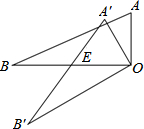如图，△AOB中，∠AOB=90°，AO=3，BO=6，△AOB绕顶点O逆时针旋转到△AOB处，此时线段A′B′与BO的交点E为BO的中点，则线段B′E的长度为$\frac{9\sqrt{5}}{5}$．