题目内容
 如图所示,P是∠AOB的角平分线OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D、E,则图中全等三角形有
如图所示,P是∠AOB的角平分线OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D、E,则图中全等三角形有考点:全等三角形的判定,角平分线的性质
专题:
分析:首先根据角平分线的性质可得PD=PE,然后再证明△PDO≌△PEO,可得DO=EO,再证明△DOF≌△EOF可得EF=FD,最后证明△PDF≌△PEF.
解答:解:△PDO≌△PEO,△PDF≌△PEF,△DOF≌△EOF,
∵P是∠AOB的角平分线OC上的一点,PD⊥OA,PE⊥OB,
∴PD=PE,∠PDO=∠PEO=90°,
在Rt△PDO和Rt△PEO中,
,
∴Rt△PDO≌Rt△PEO(HL),
∴DO=EO,
∵P是∠AOB的角平分线OC上的一点,
∴∠POD=∠POE,
在△DOF和△EOF中,
,
∴△DOF≌△EOF(SAS),
∴EF=FD,
在△PDF和△PEF中,
,
∴△PDF≌△PEF(SSS).
故答案为:△PDO≌△PEO,△PDF≌△PEF,△DOF≌△EOF.
∵P是∠AOB的角平分线OC上的一点,PD⊥OA,PE⊥OB,
∴PD=PE,∠PDO=∠PEO=90°,
在Rt△PDO和Rt△PEO中,
|
∴Rt△PDO≌Rt△PEO(HL),
∴DO=EO,

∵P是∠AOB的角平分线OC上的一点,
∴∠POD=∠POE,
在△DOF和△EOF中,
|
∴△DOF≌△EOF(SAS),
∴EF=FD,
在△PDF和△PEF中,
|
∴△PDF≌△PEF(SSS).
故答案为:△PDO≌△PEO,△PDF≌△PEF,△DOF≌△EOF.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
以下对|1+3|的解释不正确的是( )
| A、数轴上点4到原点的距离 |
| B、数轴上点1到点-3的距离 |
| C、数轴上点1及点-3到原点的距离之和 |
| D、数轴上点1到点3的距离 |
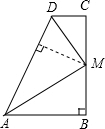 如图,AB⊥BC,CD⊥BC,M是BC上的一点,连接DM、AM,且AM、DM分别平分∠DAB和∠ADC,试判断BM和CM的大小关系,并说明理由.
如图,AB⊥BC,CD⊥BC,M是BC上的一点,连接DM、AM,且AM、DM分别平分∠DAB和∠ADC,试判断BM和CM的大小关系,并说明理由.