题目内容
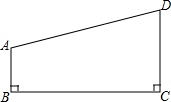 如图,已知在梯形ABCD中,AB∥CD,∠B=90°,AB=3,BC=11,DC=6,P为BC边上一点,使得△ABP与△PCD相似,求BP的长及△ABP与△PCD的面积比.
如图,已知在梯形ABCD中,AB∥CD,∠B=90°,AB=3,BC=11,DC=6,P为BC边上一点,使得△ABP与△PCD相似,求BP的长及△ABP与△PCD的面积比.考点:相似三角形的判定
专题:
分析:首先设BP=x,然后分别从当
=
,即
=
时,△ABP∽△DCP与当
=
,即
=
时,△ABP∽△PCD去分析求解即可求得答案.
| AB |
| CD |
| BP |
| CP |
| 3 |
| 6 |
| x |
| 11-x |
| AB |
| CP |
| BP |
| CD |
| 3 |
| 11-x |
| x |
| 6 |
解答: 解:∵AB∥CD,∠B=90°,
解:∵AB∥CD,∠B=90°,
∴∠C=∠B=90°,
设BP=x,则CP=BC-BP=11-x,
①当
=
,即
=
时,△ABP∽△DCP,
解得:x=
,
∴BP=
,CP=11-
=
,
∴S△ABP:S△CDP=1:4;
②当
=
,即
=
时,△ABP∽△PCD,
解得:x1=2,x2=9,
∴BP=2或BP=9,
当BP=2时,S△ABP:S△CDP=1:9,
当BP=9时,S△ABP:S△CDP=9:4.
 解:∵AB∥CD,∠B=90°,
解:∵AB∥CD,∠B=90°,∴∠C=∠B=90°,
设BP=x,则CP=BC-BP=11-x,
①当
| AB |
| CD |
| BP |
| CP |
| 3 |
| 6 |
| x |
| 11-x |
解得:x=
| 11 |
| 3 |
∴BP=
| 11 |
| 3 |
| 11 |
| 3 |
| 22 |
| 3 |
∴S△ABP:S△CDP=1:4;
②当
| AB |
| CP |
| BP |
| CD |
| 3 |
| 11-x |
| x |
| 6 |
解得:x1=2,x2=9,
∴BP=2或BP=9,
当BP=2时,S△ABP:S△CDP=1:9,
当BP=9时,S△ABP:S△CDP=9:4.
点评:此题考查了相似三角形的判定.此题难度适中,注意掌握数形结合思想、分类讨论思想与方程思想的应用.

练习册系列答案
相关题目
A、B两城相距720km,普快列车从A城出发120km后,特快列车从B城开往A城,6h后两车相遇.若普快列车是特快列车速度的
,且设普快列车速度为xkm/h,则下列所列方程错误的是( )
| 2 |
| 3 |
A、720-6x=6×
| ||
B、720+120=6(x+
| ||
C、6x+6×
| ||
D、6(x+
|
以下对|1+3|的解释不正确的是( )
| A、数轴上点4到原点的距离 |
| B、数轴上点1到点-3的距离 |
| C、数轴上点1及点-3到原点的距离之和 |
| D、数轴上点1到点3的距离 |
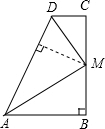 如图,AB⊥BC,CD⊥BC,M是BC上的一点,连接DM、AM,且AM、DM分别平分∠DAB和∠ADC,试判断BM和CM的大小关系,并说明理由.
如图,AB⊥BC,CD⊥BC,M是BC上的一点,连接DM、AM,且AM、DM分别平分∠DAB和∠ADC,试判断BM和CM的大小关系,并说明理由.