题目内容
15. 如图,直线L上有三个正方形a,b,c,若a,c的面积分别为1和9,则b的面积为( )
如图,直线L上有三个正方形a,b,c,若a,c的面积分别为1和9,则b的面积为( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
分析 运用正方形边长相等,再根据同角的余角相等可得∠BAC=∠DCE,然后证明△ACB≌△DCE,再结合全等三角形的性质和勾股定理来求解即可.
解答 解:由于a、b、c都是正方形,所以AC=CD,∠ACD=90°;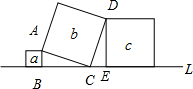
∵∠ACB+∠DCE=∠ACB+∠BAC=90°,即∠BAC=∠DCE,
在△ABC和△CED中,
$\left\{\begin{array}{l}{∠ABC=∠DEC=90°}\\{∠ACB=∠CDE}\\{AC=DC}\end{array}\right.$,
∴△ACB≌△DCE(AAS),
∴AB=CE,BC=DE;
在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=AB2+DE2,
即Sb=Sa+Sc=1+9=10,
∴b的面积为10,
故选C.
点评 此题主要考查对全等三角形和勾股定理的综合运用,关键是证明△ACB≌△DCE.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
6.下列事件是必然事件的是( )
| A. | 明天太阳从西边升起 | |
| B. | 掷出一枚硬币,正面朝上 | |
| C. | 打开电视机,正在播放“新闻联播” | |
| D. | 任意画一个三角形,它的内角和等于180° |
3.抛物线y=x2+kx-1与x轴交点的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 以上都不对 |
7.下列方程中,是一元一次方程的是( )
| A. | 3x+2y=7 | B. | 3x2-2x=1 | C. | x-2=3 | D. | x-1=$\frac{1}{x}$ |