题目内容
7.函数y=x+5的图象与反比例函数y=$\frac{-2}{x}$的图象的一个交点为A(a,b),则$\frac{1}{a}$-$\frac{1}{b}$=-2.5.分析 把A点坐标分别代入一次函数和反比例函数,可得到关于a、b的代数式,可求得ab和b-a的值,代入可求得答案.
解答 解:∵A为两函数图象的交点,
∴把A点坐标代入两函数解析式可得$\left\{\begin{array}{l}{b=a+5}\\{b=-\frac{2}{a}}\end{array}\right.$,
∴ab=-2,b-a=5,
∴$\frac{1}{a}$-$\frac{1}{b}$=$\frac{b-a}{ab}$=$\frac{5}{-2}$=-2.5,
故答案为:-2.5.
点评 本题主要考查函数图象的交点,掌握两函数图象的交点坐标满足每一个函数解析式是解题的关键,注意整体思想的应用.

练习册系列答案
相关题目
18.2的相反数和绝对值分别是( )
| A. | 2,2 | B. | -2,2 | C. | -2,-2 | D. | 2,-2 |
15.下列事件中,是随机事件的为( )
| A. | 水涨船高 | B. | 守株待兔 | C. | 水中捞月 | D. | 冬去春来 |
12.已知一个二元一次方程组的解是$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,则这个方程组是( )
| A. | $\left\{\begin{array}{l}{x+y=-3}\\{xy=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=-3}\\{x-2y=1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{2x=y}\\{y-x=-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{2}{3x}-\frac{5}{6y}=1}\\{2x+y=-4}\end{array}\right.$ |
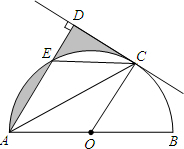 如图,AB是⊙O直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连CE.
如图,AB是⊙O直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连CE. 如图,经过平移,小船上的点A移到了点B的位置,请画出平移后的小船.
如图,经过平移,小船上的点A移到了点B的位置,请画出平移后的小船.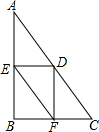 如图,△ABC中,∠B=90°,AB=8,BC=6,点D是AC上的任意一点,过点D作DE⊥AB于点E,DF⊥BC于点F,连接EF,则EF的最小值是4.8.
如图,△ABC中,∠B=90°,AB=8,BC=6,点D是AC上的任意一点,过点D作DE⊥AB于点E,DF⊥BC于点F,连接EF,则EF的最小值是4.8.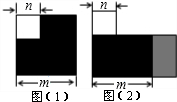 小明同学将图(1)中的阴影部分(边长为m的大正方形中有一个边为n的小正方形)拼成了一个长方形(如图2),比较两个图的面积可以得出的结论是m2-n2=(m+n)(m-n) (用含m,n的式子表达)
小明同学将图(1)中的阴影部分(边长为m的大正方形中有一个边为n的小正方形)拼成了一个长方形(如图2),比较两个图的面积可以得出的结论是m2-n2=(m+n)(m-n) (用含m,n的式子表达)