题目内容
3.先化简再求值:$\frac{a-2}{{{a^2}-1}}÷(\frac{1}{a-1}-a-1)$,其中a是方程x2+3x-1=0的解.分析 先算括号里面的,再算除法,求出a的值代入进行计算即可.
解答 解:原式=$\frac{a-2}{(a+1)(a-1)}$÷$\frac{2-a}{a-1}$
=$\frac{a-2}{(a+1)(a-1)}$•$\frac{a-1}{2-a}$
=-$\frac{1}{a+1}$,
∵a是方程x2+3x-1=0的解,
∴a2+3a-1=0,解得a=$\frac{-3±\sqrt{13}}{2}$,
当a=$\frac{-3+\sqrt{13}}{2}$时,原式=-$\frac{1}{\frac{-3+\sqrt{13}}{2}+1}$=-$\frac{\sqrt{13}+1}{6}$;
当a=$\frac{-3-\sqrt{13}}{2}$时,原式=-$\frac{1}{\frac{-3-\sqrt{13}}{2}+1}$=-$\frac{\sqrt{13}-1}{6}$.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
相关题目
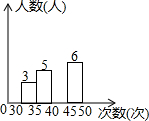 为了解某校八年级女生1分钟仰卧起坐的次数,从中随机揣测了50名女生参加1分钟仰卧起坐的次数测试,并绘制成一个不完整的频数分布直方图(如图),则1分钟仰卧起坐的次数在40-45的频率是0.72.
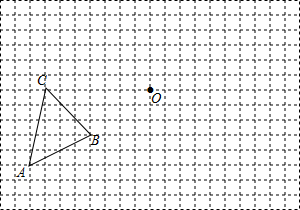
为了解某校八年级女生1分钟仰卧起坐的次数,从中随机揣测了50名女生参加1分钟仰卧起坐的次数测试,并绘制成一个不完整的频数分布直方图(如图),则1分钟仰卧起坐的次数在40-45的频率是0.72. 已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′
已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′