题目内容
13.先化简,再求值:(a-$\frac{2a}{a+1}$)÷$\frac{{a}^{2}-2a+1}{{a}^{2}-1}$-a2,其中a是方程x2-x-3=0的解.分析 先对原式化简,再根据a是方程x2-x-3=0的解,可以求得出a的值,代入化简后的式子即可解答本题.
解答 解:(a-$\frac{2a}{a+1}$)÷$\frac{{a}^{2}-2a+1}{{a}^{2}-1}$-a2
=$\frac{a(a+1)-2a}{a+1}×\frac{(a+1)(a-1)}{(a-1)^{2}}-{a}^{2}$
=$\frac{{a}^{2}+a-2a}{a-1}$-a2
=$\frac{a(a-1)}{a-1}$-a2
=a-a2,
∵x2-x-3=0,
解得,x=$\frac{1±\sqrt{(-1)^{2}-4×1×(-3)}}{2}$=$\frac{1±\sqrt{13}}{2}$,
∵a是方程x2-x-3=0的解,
∴a=$\frac{1±\sqrt{13}}{2}$,
∴当a=$\frac{1+\sqrt{13}}{2}$时,原式=$\frac{1+\sqrt{13}}{2}-(\frac{1+\sqrt{13}}{2})^{2}$=-3,
当a=$\frac{1-\sqrt{13}}{2}$时,原式=$\frac{1-\sqrt{13}}{2}-(\frac{1-\sqrt{13}}{2})^{2}$=-3,
即原式=-3.
点评 本题考查分式的化简求值,解题的关键是明确分式的化简求值的方法.

练习册系列答案
相关题目
4.要使分式$\frac{x-1}{x-2}$有意义,则x的取值应满足( )
| A. | x≠2 | B. | x≠1 | C. | x=2 | D. | x=1 |
8.某商场购进一批名牌衬衫,要求一等品的数量12850件左右,请问该商场应购进多少件这样的衬衫?下面是该部门经理随机抽查一些衬衫后,统计得到的一等品的频率变化表:
(1)把表格补充完整(结果保留两位小数);
(2)任意抽取1件衬衫,抽得一等品的概率约为多少?
(3)你能求得商场应购进多少件这样的衬衫吗?
| 抽查数n | 100 | 200 | 1500 | 2000 | 2500 |
| 一等品数m | 94 | 194 | 1430 | 1902 | 2375 |
| 一等品频率$\frac{m}{n}$ | 0.94 | 0.97 | 0.95 | 0.95 | 0.95 |
(2)任意抽取1件衬衫,抽得一等品的概率约为多少?
(3)你能求得商场应购进多少件这样的衬衫吗?
18.已知一个三角形的两边长分别为2cm和4cm,第三边的长为偶数,则第三边的长为( )
| A. | 2cm | B. | 3cm | C. | 4cm | D. | 6cm |
17.已知等腰三角形的底边长为10,腰长为13,则一腰上的高为( )
| A. | 12 | B. | $\frac{60}{13}$ | C. | $\frac{120}{13}$ | D. | $\frac{13}{5}$ |
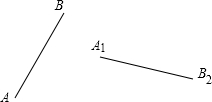 如图,线段AB绕点O顺时针旋转一定的角度得到线段A1B1(点A的对应点为A1).
如图,线段AB绕点O顺时针旋转一定的角度得到线段A1B1(点A的对应点为A1).